RESUMEN
Introducción: El
artículo presenta el cálculo de amplitudes de ángulos, como una de las
habilidades matemáticas a lograr en los estudiantes de séptimo grado y en tal
sentido, brinda una respuesta a la contradicción que existe entre las
exigencias planteadas para el desarrollo de la habilidad correspondiente y los
niveles de desarrollo que se alcanzan en la práctica. Objetivo: ofrecer un
procedimiento didáctico para el desarrollo de la habilidad “calcular amplitudes
de ángulos” en los estudiantes de séptimo grado. Métodos: se utilizaron métodos
teóricos que permitieron profundizar en las características del proceso de
enseñanza-aprendizaje de la Matemática y en particular, de la geometría y del
proceso de desarrollo de una habilidad. También, se emplearon métodos empíricos
para conocer los resultados que se obtienen al utilizar el procedimiento en la
práctica pedagógica. Resultado: se ofrece un procedimiento didáctico, que
permite orientar el trabajo planificado de los estudiantes durante la solución
de ejercicios y problemas de cálculo de amplitudes de ángulos. Conclusiones:
su aplicación en la práctica evidenció resultados favorables en
el nivel de desarrollo de la habilidad “calcular amplitudes de ángulos” en los
estudiantes que formaron parte de la investigación.
Palabras clave: amplitudes de ángulos; geometría; habilidad; matemática; procedimiento
didáctico; proceso de enseñanza-aprendizaje.
______________________________ABSTRACT
The article presents calculating the size of
angles as one of the mathematical skills to develop in seventh grade students.
Accordingly, it offers an answer to the existing contradiction between the
requirements to develop the skill and the level attained in practice. Objective:
to offer a teaching strategy for the development of the skill "to
calculate the size of angles" in seventh grade students. Methodology:
Theoretical methods were used to thoroughly address the characteristics of the
Mathematics teaching-learning process, specifically geometry and the skill
development process. In addition, empirical methods allowed to analyze the results
of the implementation of the teaching strategy. Results: A teaching
strategy to guide the students´ performance when solving mathematical problems
about calculating the size of angles. Conclusions: The implementation of
the strategy showed favorable results as to developing the skill "to
calculate the size of angles" in the students that were part of the research.
Keywords:
size of angles; geometry;
mathematical skill; teaching strategy; teaching-learning process.
INTRODUCCIÓN
a
formación integral de las nuevas generaciones es una tarea cada vez más
compleja e importante para los pedagogos de estos tiempos. Al respecto, se
reconoce que el mundo desde los inicios del siglo XXI está marcado por complejos
procesos de cambios, transformaciones o reajustes sociales en los cuales juega
un rol fundamental la educación.
En
este sentido, se advierte que para una adecuada inclusión y protagonismo de los
sujetos en la vida moderna es necesario apropiarse de determinados saberes que
permitan la convivencia en las actuales condiciones sociales. Es preciso,
entonces, desarrollar en los estudiantes el saber hacer; de ahí la importancia
que se concede al proceso de formación y desarrollo de habilidades que posibiliten
la aplicación responsable y creadora de los conocimientos en una diversidad de
tipos de tareas y contextos.
Al
ser consecuente con las ideas expresadas, el proceso de enseñanza-aprendizaje
de la Matemática en la Secundaria Básica debe contribuir a la formación de
ciudadanos cada vez más cultos, y para ello, aprovechar las potencialidades de
sus contenidos. En este nivel de educación, es imprescindible que los
estudiantes asuman roles protagónicos en aras de lograr aprendizajes cada vez
más desarrolladores que le estimulen el saber hacer, de ahí la importancia de
desarrollar las habilidades específicas de esta asignatura.
Para
el tratamiento de la geometría, resultan de interés los criterios de autores
extranjeros y nacionales. León, Ripamonti y Flores (2020) precisan sobre la
importancia de la indagación y el trabajo colaborativo para el aprendizaje
dinámico de la geometría; Riascos (2019) profundiza en la formación de
conceptos geométricos; Varela (2018) insiste en el desarrollo de la
visualización espacial mediante el aprendizaje de la geometría. Por otra parte,
Álvarez, Almeida y Villegas (2014) destacan el cálculo de amplitudes de ángulo
como un objetivo fundamental de la enseñanza de la geometría. Ninguno de ellos
analizó el desarrollo de la habilidad “calcular amplitudes de ángulos” y,
tampoco, explicitan en sus trabajos un procedimiento que oriente el accionar de
los estudiantes al calcular amplitudes de ángulos.
Al
profundizar, en la práctica pedagógica de la ESBU “Mártires de La Sierpe”, en la
problemática anterior fue posible comprobar en los informes de los controles a
clases (5) y de las comprobaciones de conocimiento aplicadas a veintidós estudiantes
de séptimo grado que aún persisten dificultades en el desarrollo de la
habilidad “calcular amplitudes de ángulos”. Entre las más significativas,
sobresalen:
·
El
limitado dominio de los conocimientos geométricos necesarios para el cálculo de
amplitudes ángulos, con énfasis en las propiedades de las figuras planas.
·
La
no comprensión adecuada de las definiciones de los diferentes tipos de ángulos
entre dos rectas cortadas por una secante.
·
El
restringido poder de identificación de los diferentes tipos de ángulos y de las
relaciones entre ellos.
·
Las
dificultades al esbozar figuras de análisis o auxiliares a partir de los datos
que ofrecen los ejercicios y de las propiedades que cumplen los objetos
geométricos que en ellos intervienen.
Ante
estas dificultades se hace necesario responder la siguiente interrogante: ¿Cómo
favorecer el desarrollo de la habilidad “calcular amplitudes de ángulos” en los
estudiantes de séptimo grado?
Para
su respuesta, los autores del artículo se proponen como objetivo: ofrecer
un procedimiento didáctico para el desarrollo de la habilidad “calcular
amplitudes de ángulos” en los estudiantes de séptimo grado.
MARCO
TEÓRICO O REFERENTES CONCEPTUALES
El
proceso de enseñanza-aprendizaje desarrollador
En
Cuba, se ha desarrollado un enfoque al que han dado en llamar “proceso de
enseñanza-aprendizaje desarrollador”, el cual responde a los cambios sociales y
tecnológicos de cada contexto y tiene la intención de promover aprendizajes
cada vez más duraderos y aplicables a nuevas situaciones de la realidad del
país.
Desde
esta posición, se asumen los criterios de Soto y García (2013) cuando destacan
que el proceso de enseñanza-aprendizaje es desarrollador, si cumple con las
siguientes exigencias:
·
Promover
el desarrollo integral de la personalidad del educando.
·
Potenciar
el tránsito progresivo de niveles de dependencia a la independencia y a la
autorregulación.
·
Desarrollar
en los escolares la capacidad de conocer, controlar y transformarse a sí y a su
medio creadoramente.
·
Desarrollar
la capacidad para realizar aprendizajes a lo largo de la vida, a partir de
poseer habilidades, hábitos y estrategias para aprender.
Igualmente,
se consideran los criterios de La Red y Rebilla (2017) al plantear que el
proceso de enseñanza-aprendizaje desarrollador es aquel que se:
Sustenta
en la concepción del desarrollo del educando a partir de sus potencialidades,
considerando los conocimientos, las habilidades, los hábitos, las capacidades,
los valores, que lo pongan en posesión de la cultura, pero tienen que
contribuir a una formación ideológica, garantizar una preparación laboral y
para la vida, propiciar una concepción científica del mundo favorecer la
formación de sentimientos y conceptos morales, una formación integral de la
sexualidad y el uso responsable y eficiente de las nuevas tecnologías de la
informática y las comunicaciones, (sistemas informáticos y audiovisuales) que
garanticen los modos de hacer, de actuar y transformar que requiere la sociedad
cubana del presente y del futuro. (p. 57).
El
enfoque metodológico del proceso de enseñanza-aprendizaje de la Matemática
La
enseñanza de las ciencias y, en particular, de la Matemática, considera las
concepciones pedagógicas contemporáneas basadas en la necesidad de un proceso
de enseñanza-aprendizaje desarrollador. En ella, se destaca la necesidad de
potenciar el aprender a hacer, aspecto en que enfatizan estudiosos de la didáctica
de la Matemática.
Al
considerar las ideas anteriores, se asume que el proceso de
enseñanza–aprendizaje de la Matemática es desarrollador si los estudiantes
logran:
· La
adquisición de los conocimientos, las habilidades y las capacidades matemáticas
requeridas para realizar aprendizajes durante toda su vida.
· El
tránsito progresivo de la dependencia a la independencia y a la autorregulación
durante la realización de diversas tareas docentes.
· El
desarrollo integral de la personalidad (Leiva, 2007).
Para
ser consecuente, los autores asumen que el aprendizaje desarrollador de la Matemática es el aquel que:
Garantiza
en el individuo la apropiación activa y creadora del saber matemático
propiciando la adquisición de los procesos de pensamiento y las formas de
trabajo propias de la Matemática, su simbología, así como destrezas,
capacidades, hábitos, convicciones que al ser estructurados en forma de
sistema, le permitan comprender y transformar el mundo que le rodea y a su vez
transformarse, potenciando el desarrollo de su independencia cognoscitiva en
estrecha relación con los necesarios procesos de socialización. (Gibert y
Ballester, 2010, p.7).
A
raíz de lo anterior, se reconoce que la enseñanza de la Matemática desde una concepción desarrolladora, tiene que promover un aprendizaje
interactivo, reflexivo y cooperativo en todos los estudiantes, sin el cual este
pierde su sentido.
Por
otra parte, la enseñanza de la Matemática juega un papel importante en la
formación integral de los estudiantes para que sean capaces de asumir los retos
científico-técnicos que demanda el actual desarrollo social. Al respecto,
Domínguez y Acosta (2016) refieren, como función de la asignatura Matemática
“la de contribuir a la educación multifacética de los educandos y al desarrollo
de sus capacidades mentales…” (p. 4).
Ante
esta exigencia, es necesario que la escuela prepare a los estudiantes para
aprender y aprender a hacer. Es por ello que, la dirección del proceso de
enseñanza-aprendizaje debe potenciar una verdadera disposición para aprender de
forma activa y estratégica, enfrentar las tareas y mantener la concentración y
los esfuerzos por lograr los objetivos propuestos, en particular, el desarrollo
de las habilidades matemáticas correspondientes.
Sobre
este tema específico, Álvarez, Almeida y Villegas (2014) plantean que resulta
necesario que desde el proceso de enseñanza-aprendizaje de la Matemática los
estudiantes adquieran una concepción científica del mundo, una cultura general
integral y un pensamiento científico. En tal sentido, refieren ideas
metodológicas que caracterizan el mencionado proceso; entre ellas destacan las
siguientes:
· Sistematizar
continuamente conocimientos, habilidades y modos de la actividad mental,
tratando además que se integre el saber de los alumnos procedente de distintas
áreas de la Matemática e incluso de otras asignaturas.
· Realizar
el diagnóstico sistemático de los conocimientos, habilidades, modos de la
actividad mental, y de las formas de sentir y actuar de los alumnos, valorando
en cada caso cuáles son las potencialidades y las causas de las dificultades de
estos, de modo que se propicien acciones de autocontrol y autovaloración y se
obtengan aprendizajes de los errores.
· Planificar,
orientar y controlar el trabajo independiente de forma sistémica, variada y
diferenciada, que les permita desarrollar habilidades para la lectura, la
búsqueda de información, la interpretación de diversas fuentes, el trabajo
cooperado y la argumentación y comunicación de sus ideas, en un adecuado clima
afectivo donde haya margen para el error. (Álvarez, Almeida y Villegas, 2014, p.1).
En
las ideas citadas, se explicita la necesidad de la formación y desarrollo de
las habilidades matemáticas; la importancia de su sistematización continúa y la
pertinencia de que al aplicarlas los estudiantes desarrollen modos de la
actividad mental propios de la actividad matemática. De ahí, que en el artículo
preste especial atención a la habilidad “calcular amplitudes de ángulos”.
El
proceso de enseñanza-aprendizaje de la Geometría
Se
inicia el apartado, compartiendo la idea de Brousseau (2003) al referir que
estudiar Geometría es importante porque contribuye al desarrollo del
pensamiento matemático de los estudiantes; pues, a su juicio, implica el uso
del razonamiento y de la imaginación deductiva, así como la visualización de
imágenes.
Igualmente,
se reconocen las potencialidades de los contenidos geométricos para el
desarrollo de actitudes y valores en los estudiantes. Sobre este particular,
Godino y Ruiz (2004) señalan que al aprender Geometría es posible desarrollar:
· La
curiosidad por identificar formas y relaciones geométricas en objetos del
entorno.
· La
perseverancia en la búsqueda de soluciones a situaciones problemáticas
relacionadas con la organización y utilización del espacio.
· El
gusto por la precisión en la descripción y representación de formas
geométricas.
· La
disposición favorable para la utilización de los instrumentos convencionales de
dibujo y para la búsqueda de instrumentos alternativos.
También,
Radillo y Huerta (2006) reconocen que el aprendizaje de la Geometría implica el
manejo de un lenguaje especializado que consta de vocabulario técnico,
símbolos, gráficas y figuras, con reglas sintácticas y semánticas definidas
para representar conceptos, propiedades y relaciones; es por ello, que estas se
articulan al describir el procedimiento que se propone para el desarrollo de la
habilidad que se analiza.
Desde
el contexto cubano, la Geometría es considerada una de las líneas directrices.
Según Álvarez, Almeida y Villegas (2014) ella “prepara a los alumnos para
orientarse en el entorno espacial, percibir sus proporciones y dimensiones,
desarrollar una memoria visual, captar semejanzas y diferencias, regularidades
y manipular mentalmente figuras geométricas, entre otros aspectos” (p. 76).
Los
mismos autores, plantean que desde el proceso de enseñanza-aprendizaje de la
Geometría los estudiantes adquieren conocimientos y habilidades, y desarrollan
un pensamiento geométrico-espacial que les permite reforzar el saber adquirido
en otras áreas y les estimula el gusto por la belleza, la limpieza y la
exactitud. De ahí, la necesidad de perfeccionar el tratamiento metodológico de
sus contenidos.
Según
plantean Acosta, Domínguez, Quintana, Gort, Báez, Cantón y Cantero (2016)
asegurar el dominio de los conocimientos geométricos, significa que los
estudiantes logran: identificar, definir y clasificar figuras planas; esbozar
figuras geométricas que satisfagan determinadas condiciones; calcular
amplitudes de ángulos; resolver ejercicios y problemas intramatemáticos y
extramatemáticos; realizar demostraciones sencillas y ejercicios de
demostración y fundamentar adecuadamente sus razonamientos.
También,
Acosta et al. (2016) destacan que: “la construcción de una figura de análisis
para apoyo en la búsqueda de la idea de solución del ejercicio o problema
geométrico garantiza la ejecución efectiva del procedimiento y la solución
correcta” (p. 32). De ahí, la importancia que se le atribuye al hecho de
esbozar y analizar una figura en la que puedan establecerse e identificar las
relaciones entre los objetos geométricos y sus propiedades.
Finalmente,
para los autores del artículo, resulta pertinente resaltar que en las
orientaciones metodológicas que se ofrecen para el tratamiento del cálculo de
amplitudes de ángulos no se precisan ideas relacionadas con el proceso de
formación y desarrollo de la habilidad “calcular amplitudes de ángulos”; es por
ello que a continuación se profundiza en la temática referida.
El
desarrollo de habilidades matemáticas. Elementos teóricos y metodológicos
Para
el análisis de la categoría habilidad, resultan de interés los criterios de
autores clásicos y cubanos que han estudiado la temática; Pérez (2015) al
estudiarlos concluyó que sus posiciones resaltan: el papel de las acciones y
operaciones sobre la base de la experiencia recibida por los sujetos, y las
relaciones entre ellas; la utilización creadora de los conocimientos, tanto
durante el proceso de actividades teóricas como prácticas; así como el dominio
de un sistema de acciones psíquicas y prácticas necesarias para la regulación
de la actividad, con ayuda de los conocimientos que la persona posee. Los
mismos, analizan las habilidades como las acciones y operaciones que realizan
los sujetos a partir de la integración de los conocimientos para su aplicación
en la práctica.
En
este artículo se asumen las habilidades como: “Un sistema de acciones y
operaciones, dominado por el sujeto, que responde a un objetivo. Es el
componente del contenido, que refleja las realizaciones del hombre en una rama
del saber propio de la cultura de la humanidad” (Álvarez, 1996, p.16).
Desde
esta perspectiva, es posible comprender las habilidades desde la teoría de la
actividad y destacar el papel de las acciones y operaciones que realiza el
sujeto a partir de la aplicación integrada de los contenidos; aunque es
pertinente esclarecer que estas últimas no constituyen un esquema rígido, ya
que dependen de las experiencias antecedentes del sujeto y del contexto social.
Resulta
indiscutible precisar, en el orden metodológico, que los estudiantes deben
reconocer las acciones que componen cada habilidad con un carácter consciente y
comprender que las operaciones se despliegan según las condiciones del
contexto. López (1990), sugiere como etapas para la adquisición de una
habilidad la de formación y el desarrollo. La primera de ellas es:
“comprendida como la adquisición consciente de los modos de actuar, cuando bajo
la dirección del maestro o profesor el alumno recibe la orientación adecuada sobre
la forma de proceder” (p. 2).
Para
el propio autor, la etapa de desarrollo de una habilidad:
Ocurre
una vez adquiridos los modos de acción, se inicia el proceso de ejercitación,
es decir, de uso de la habilidad recién formada en la cantidad necesaria y con
una frecuencia adecuada, de modo que vaya haciéndose cada vez más fácil de
reproducir o usar, y se eliminen los errores; son indicadores de un buen
desarrollo la rapidez y corrección con que la acción se ejecute. (López, 1990,
p. 2).
Dadas
las particularidades de cada etapa, se identifica la estrecha unidad entre
acciones y operaciones y se precisa, que entre ellas se establece una estrecha
relación dialéctica (Silvestre y Zilberstein, 2002). Al coincidir con este
criterio, se reconoce que las habilidades forman un sistema, unas son más
complejas que otras, y que para desarrollarlas se requiere primero formar las
subordinadas, e incluso unas pueden constituir parte del sistema de acciones de
las otras.
Estos
elementos teóricos, toman un matiz diferente sin son analizados, en particular,
para las habilidades matemáticas específicas. Sobre este particular, Ferrer y
Rebollar (1999) plantean que la concepción del proceso de formación y
desarrollo de habilidades matemáticas no solo debe atender al sistema de
acciones y operaciones correspondientes, sino que es preciso tener en cuenta la
actuación del sujeto, su actitud y disposición hacia la apropiación de la
actuación correspondiente.
Estos
autores, señalaron que las habilidades matemáticas tienen como premisas lograr
claridad acerca del objeto matemático sobre el que actúa el individuo
(procedimiento de solución) y la delimitación de las acciones que sobre dicho
objeto va a ejecutar según el propósito o fin a lograr. Esto obliga a reflexionar
sobre el significado que en el orden intelectual y lógico tiene una u otra acción.
Desde estas posiciones, se asume que una habilidad matemática:
Es
la construcción, por el alumno, del modo de actuar inherente a una determinada
actividad matemática, que le permite buscar o utilizar conceptos, propiedades,
relaciones, procedimientos matemáticos, utilizar estrategias de trabajo,
realizar razonamientos, juicios que son necesarios para resolver problemas
matemáticos. (Ferrer y Rebollar, 1999, p. 25).
Siendo
consecuente con este criterio, los autores insisten en proponer como posible
vía de solución a la problemática identificada un procedimiento didáctico.
Por
otra parte, se reconoce que el desarrollo de las habilidades matemáticas
constituye un proceso en el que se estructura y reestructura el sistema de
acciones y en esa reestructuración o transformación estructural se alcanzan
estados superiores lo que significa que cada nueva habilidad se incorpora al
sistema ya formado, pero no como una habilidad más, sino como un elemento que
aporta nuevas interpretaciones, racionaliza procesos u ofrece otras variantes
de solución que no borra los sistemas formados, sólo los enriquece.
El
contenido de una habilidad matemática refleja la exigencia en cuanto a la
sistematización de las habilidades referidas a la elaboración o utilización de
conceptos, propiedades, procedimientos algorítmicos o heurísticos que
posibilitan el desarrollo de la habilidad general correspondiente.
Un
ejemplo de habilidad matemática básica es precisamente: “calcular amplitud de
ángulos”, la misma se relaciona o responde a la habilidad matemática general
“resolver problemas geométricos”; en este trabajo los autores ofrecen un
procedimiento para su desarrollo.
Según
las posiciones teóricas analizadas, se considera que la habilidad matemática
“calcular amplitudes de ángulos” está determinada por las invariantes:
identificar el o los ángulos cuyas amplitudes se tiene que calcular, reconocer
las propiedades geométricas que cumplen los objetos geométricos de la figura
(dada o esbozada), establecer relaciones entre el o los ángulos cuyas amplitudes
se tiene que calcular con otros de la figura, calcular la amplitud del o de los
ángulos pedidos y fundamentar la relación que existe entre ellos y los
utilizados.
METODOLOGÍA EMPLEADA
La
metodología seguida al elaborar la posible vía de solución que se propone para
la problemática identificada se caracterizó por un enfoque cuantitativo.
Primeramente,
se utilizaron métodos teóricos como el histórico-lógico y el analítico-sintético;
los que posibilitaron fundamentar el proceso de enseñanza-aprendizaje de la
Matemática y el tratamiento de la categoría habilidad. De igual forma,
permitieron esclarecer el diseño del procedimiento didáctico y las relaciones
entre sus acciones.
También
se utilizaron métodos empíricos, entre ellos destacan el análisis del producto
de la actividad, la observación pedagógica y la entrevista. Estos facilitaron la
recogida y el análisis de datos relacionados con el proceso de enseñanza-aprendizaje
de los contenidos geométricos correspondientes y sus resultados, como elemento
esencial para esclarecer el estado de la problemática objeto de análisis y
posterior a la aplicación práctica de la propuesta.
RESULTADOS Y DISCUSIÓN
Para
presentar la propuesta que realizan los autores del presente artículo se tiene
en cuenta que los procedimientos son: “herramientas que le permiten alcanzar un
fin a partir del cumplimiento de una secuencia de pasos con un orden lógico y
coherente” (Zilberstein y Silvestre, 2004, p. 20).
De
igual forma se analiza que los procedimientos didácticos constituyen:
Herramientas
que le permiten al docente orientar y dirigir la actividad del alumno, de modo
tal que la influencia de los "otros", propicie el desarrollo
individual, estimulando el pensamiento
lógico, el pensamiento teórico y la independencia
cognitiva, motivándolo a "pensar" en un "clima favorable de
aprendizaje. (Zilberstein y Silvestre, 2004, p. 99)
De
ahí que, el procedimiento didáctico que se propone para el desarrollo de la
habilidad “calcular amplitudes de ángulos” consista en:
·
Identificar
en la figura (que ofrece el ejercicio o se construye) el o los ángulos cuyas
amplitudes se tiene que calcular.
·
Reconocer
y comprender la información que brinda el ejercicio y las propiedades
geométricas que cumplen los objetos de la figura.
·
Relacionar
el o los ángulos cuyas amplitudes se debe calcular con otros que, a partir de
las condiciones del ejercicio, se conozca su amplitud.
·
Calcular
y fundamentar la relación entre el ángulo a calcular y el o los ángulos de la
figura (dada o elaborada) utilizados para obtener la amplitud del primero.
(Iznaga, 2016, p. 25).
A
continuación, se muestran varios ejemplos de la aplicación de las acciones del
procedimiento a la solución de ejercicios.
Ejemplo
1
Selecciona la
respuesta correcta:
Sean
α y β dos ángulos adyacentes y α = 280, entonces: β
= 820 β = 280 β = 1520
Acción 1
El
estudiante debe construir la figura de análisis a partir de la definición de
ángulos adyacentes e identificar el ángulo cuya amplitud debe calcular.

Acción
2
El
estudiante debe identificar la propiedad de los ángulos adyacentes, es decir: la
suma de sus amplitudes es 1800
Acción
3
El
estudiante debe aplicar la propiedad de los ángulos adyacentes, es decir:
<
β + < α = 1800
Acción
4
<
β + < α = 1800 por ser ángulos adyacentes
<
β = 1800 - < α
<
β = 1800 – 280
<
β = 1520
Ejemplo
2
Calcula
la amplitud de los ángulos < CAD y < CAB, teniendo en cuenta las
amplitudes de los ángulos que se dan y que las saetas indican rectas
paralelas.
<
ABC = 480, < ACB = 670
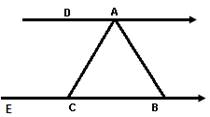
Acción 1
El
estudiante identifica los ángulos cuya amplitud tiene que calcular en la figura
y la secante con la que deberá trabajar

Acción
2
El
estudiante debe saber que en la figura:
<
ABC, < BAC y < BCA son ángulos interiores del triángulo ABC
<
ECA es un ángulo exterior del triángulo ABC o adyacente con el ángulo BCA
Acción
3
Vía
1: El estudiante debe aplicar que:
<
ABC + < BAC + < BCA = 1800
480 + < BAC + 670 = 1800
<
ECA = < CBA + < CAB o
<
ECA = 1800 - < ACB
Vía
2: Si considera las rectas paralelas puede aplicar entonces lo siguiente:
<
BCA = < CAD por ser alternos entre las paralelas y la secante CA, luego:
<
ECA + < CAD = 1800 por ser
conjugados entre las paralelas y la secante CA
Acción
4
Vía
1: < ABC + < BAC + < BCA = 1800 por suma de ángulos
interiores del triángulo ABC
480 + < BAC + 670 = 1800
< BAC = 1800 - 480 - 670
< BAC = 1800 - 1150
<
BAC = 650
<
ECA = < CBA + < CAB por ser ángulo exterior del triángulo
ABC
<
ECA = 480
+ 650 = 1130
<
ECA + < ACB = 1800
<
ECA = 1800 - < ACB
<
ECA = 1800 - 670
<
ECA = 1130
Vía
2: Si consideró las rectas paralelas:
<
BCA = < CAD por ser alternos entre las paralelas y la secante CA, luego:
<
CAD = 670
<
ECA + < CAD = 1800 por ser
conjugados entre las paralelas y la secante CA
<
ECA + 670 = 1800
<
ECA = 1800 - 670
<
ECA = 1130
RESULTADOS DE LA
APLICACIÓN PRÁCTICA DEL PROCEDIMIENTO
El procedimiento didáctico elaborado se aplicó en la práctica
pedagógica, por uno de los autores del artículo. A continuación, se describen
los principales resultados obtenidos. La experiencia se realizó en un grupo de 30
estudiantes de 7. Grado de la ESBU Mártires de La Sierpe, la misma tenía la finalidad
de determinar el nivel de desarrollo de la habilidad “calcular amplitudes de
ángulos” que ellos lograban.
Para
su evaluación se utilizaron los siguientes indicadores: conocimiento de las
acciones del procedimiento didáctico, identificación de los ángulos cuya
amplitud debían calcular, aplicación de las propiedades de los objetos geométricos
de la figura y fundamentación de las relaciones entre los ángulos cuyas
amplitudes debían calcular y otros que aparecen en la figura.
La medición
de los indicadores se realizó mediante una escala ordinal que considera las
categorías muy adecuado (MA), adecuado (A) e inadecuado (I). El proceso de
aplicación inició luego de asegurar las condiciones necesarias para la
utilización del procedimiento; para ello, se elaboró un material docente y una
lámina que describía el procedimiento.
Posteriormente,
se determinó en qué momento del sistema de clases de la asignatura se aplicaría
el procedimiento didáctico y cómo se evaluarían las transformaciones que
ocurrían en el desarrollo de la habilidad “calcular amplitudes de ángulos” en
los estudiantes. Durante la aplicación se utilizó una guía de observación para
valorar sistemáticamente la actuación de los estudiantes durante la realización
de cada ejercicio y al concluir se aplicó una prueba pedagógica.
La
evaluación sistemática de la actuación de los estudiantes durante la
realización ejercicios de cálculo de amplitudes de ángulos, realizada a partir
de la observación, permitió conocer que:
· El
96,7% (29) de los estudiantes conoce las acciones del procedimiento, el por
ciento restante aún confundía la acción relacionada con la fundamentación.
· El
93,3% (28) de los estudiantes identifican correctamente los ángulos cuya
amplitud debían calcular.
· El
93,3% (28) de los estudiantes aplica las propiedades de los objetos
representados en las figuras en general, los demás no las conoce o no comprende
su significado.
· El
90% (27) de los estudiantes fundamenta las relaciones entre los ángulos cuyas
amplitudes debían calcular y otros de la figura; el por ciento restante no
identifica bien los tipos de ángulos formados entre dos rectas paralelas y una
secante, ni sus propiedades.
Por
otra parte, en la prueba pedagógica aplicada se obtuvieron los siguientes
resultados:
· El
100 % (30) de los estudiantes conoce las acciones del procedimiento y comprende
que debe hacer en cada una de ellas.
· El
96,7 % (29) de los estudiantes logra identificar correctamente los ángulos cuyas
amplitudes debían calcular y los ubica en las figuras dadas o elaboradas.
· El
90 % (27) de los estudiantes aplica las propiedades geométricas que debe
utilizar para calcular las amplitudes de los ángulos.
· El
83,3% (25) de los estudiantes establece y fundamenta adecuadamente las
relaciones entre los ángulos cuyas amplitudes debían calcular y otros que
aparecen en la figura.
Al
triangular los resultados de los indicadores evaluados en ambos instrumentos, se
puede concluir que el 83,3 % (25) de los estudiantes logra un nivel bastante
adecuado del desarrollo de la habilidad “calcular amplitudes de ángulos”; aun
cuando se identifican dificultades en los aspectos relacionados con el dominio
de las propiedades geométricas y su fundamentación al utilizarlas para el cálculo
de amplitudes de ángulos.
Por
tal motivo, se considera oportuno plantear que el procedimiento didáctico
elaborado favorece el desarrollo de la habilidad “calcular amplitudes de
ángulos” y, por tanto, se convierte en una vía de solución a la problemática
planteada al inicio por los autores del artículo.
CONCLUSIONES
Las posiciones teóricas que
fundamentan el proceso de enseñanza-aprendizaje desarrollador y en particular,
las ideas que caracterizan el enfoque metodológico de la asignatura Matemática
se convierten en pautas a considerar para el desarrollo de la habilidad
“calcular amplitudes de ángulos”; e igualmente, justifican la precisión de las
acciones de dicha habilidad y del procedimiento didáctico que emerge como vía
de solución a la problemática de que trata el presente artículo.
El procedimiento didáctico
propuesto para favorecer el desarrollo de la habilidad “calcular
amplitudes de ángulos” se fundamenta en las exigencias del enfoque metodológico
general de la asignatura, y sus acciones orientan el trabajo planificado de los
estudiantes durante la solución de los ejercicios y problemas a partir del empleo
de formas de trabajo y de pensamiento matemático.
La aplicación del
procedimiento didáctico propuesto en la práctica pedagógica demuestra que se
logró transformar el nivel de desarrollo de la habilidad “calcular amplitudes
de ángulos” en los estudiantes que formaron parte de la muestra utilizada.
REFERENCIAS
BIBLIOGRÁFICAS
Acosta,
S., Domínguez, O., Quintana, A., Gort, M., Báez, L., Cantón, J. y Cantero, R.
(2016). Orientaciones metodológicas de Matemática Séptimo Grado. La
Habana, Cuba. Material en soporte digital.
Álvarez,
M., Almeida, B. y Villegas, E. V. (2014). El proceso de enseñanza-aprendizaje
de la asignatura matemática: Documentos metodológicos. La Habana, Cuba:
Editorial Pueblo y Educación.
Álvarez,
C. M. (1996). Diseño Curricular. Instituto Pedagógico Latinoamericano y
Caribeño. Cátedra Unesco en Ciencias de la Educación. Material impreso.
Brousseau,
G. (2003). Les propriétés didactiques de la géométrie élémentaire: l’étude
de l’espace et de la géométrie. Recuperado de http://dipmat.math.unipa.it/~grim/home
brousseau.htm
Domínguez,
O. y Acosta, S. (2016). Programa de Matemática Séptimo Grado. La Habana,
Cuba. Material en soporte digital.
Ferrer,
M. y Rebollar, A. (1999). Cómo dirigir el proceso de formación de
habilidades matemáticas. Curso 62. La Habana, Cuba: Instituto Superior
Pedagógico Frank País García.
Gibert,
E. M. y Ballester, P. (2010). Una alternativa desarrolladora para la
estructuración de la clase de matemática de la secundaria básica [CD-ROM
Evento Provincial Didáctica de las Ciencias]. La Habana, Cuba: Universidad Pedagógica
“Enrique José Varona”.
Godino,
J. D. y Ruíz, F. (2004). Geometría y su didáctica para maestros.
Proyecto Edumat-Maestros. Universidad de Granada, España. Recuperado de http://www.ugr.es/local/jgodino/edumat-maestros/www.ug
Iznaga,
Y. (2016). Procedimiento didáctico para
favorecer el desarrollo de la habilidad “calcular amplitud de ángulos” en los
estudiantes de séptimo grado (Tesis de pregrado).
Universidad de Sancti Spíritus “José Martí Pérez”, Sancti Spíritus, Cuba.
La
Red, Z. y Rebilla, A. (2017). El perfeccionamiento en el nivel educativo de
Secundaria Básica en Cuba. [CD-ROM Evento Internacional de Secundaria Básica].
La Habana,
Cuba.
Leiva,
C. S. (2007). La Evaluación de los Conocimientos y Habilidades en los
Contenidos Didácticos en la Formación Inicial de los Profesionales de la
Educación (Tesis de maestría). Universidad de Holguín “José de la
Luz y Caballero”, Holguín, Cuba.
León,
I., Ripamonti, C. y Flores, B. (2020). Geometría dinámica en la formación de
profesores, despertando el asombro a través de la indagación. Acta
Latinoamericana de Matemática Educativa, 33(1).
López,
M. (1990). Saber enseñar a describir, definir y argumentar. La Habana,
Cuba: Editorial Pueblo y Educación.
Pérez,
A. (2015). La integración de las invariantes de la habilidad profesional
planificar el proceso de enseñanza-aprendizaje desde la didáctica de la
matemática (Tesis doctoral). Universidad de Sancti Spíritus “José Martí
Pérez”, Sancti Spíritus, Cuba.
Radillo,
M. y Huerta, S. (2006). Obstáculos en el aprendizaje de la Geometría
euclideana, relacionados con la traducción entre códigos del lenguaje
matemático. En Experiencias, propuestas y reflexiones para la clase de
Matemática. Recuperado de http://www.comie.org.mx/congreso/memoriaelectronica/v09/ponencias/at01/PRE1178673333.pdf
Riascos,
Y. (2019). La formación de los conceptos de la geometría plana mediada por
ambientes dinámicos (Tesis doctoral). Universidad de Cienfuegos “Carlos
Rafael Rodríguez”, Cuba.
Silvestre,
M. y Zilberstein, J. (2002). Diagnóstico y transformación de la institución
docente. México: Ediciones CEIDE.
Soto,
M. y García, A. (2013). El aprendizaje escolar un reto para la escuela
contemporánea. Curso 27. La Habana, Cuba: Sello Editor Educación Cubana.
Varela,
N. (2018). La enseñanza- aprendizaje de la geometría y la visualización
espacial del estudiante. [CD-ROM
Congreso Internacional Universidad 2018]. Ecuador:
Universidad Católica de Santiago de Guayaquil.
Zilberstein, J. y Silvestre, M. (2004). Didáctica
desarrolladora desde el enfoque histórico cultural. México: Ediciones
CEIDE.