
ARTICULO DE INVESTIGACIÓN ORIGINAL
Fecha de presentación: 1-03-2021 Fecha de aceptación: 15-04-2021 Fecha
de publicación: 9-07-2021
LA
TRANSFERENCIA ENTRE REPRESENTACIONES VERBALES DEL PLANO EN LA FORMACIÓN DE
PROFESORES DE MATEMÁTICA
THE
TRANSFERENCE BETWEEN VERBAL REPRESENTATIONS OF PLANES IN THE TRAINING OF MATHEMATICS
PROFESSORS
Ortelio Nilo Quero-Méndez 1,
Aldo Medardo Ruiz-Pérez 2
¹Doctor en Ciencias
Pedagógicas. Profesor Titular del departamento de Física-Matemática.
Universidad de Sancti Spíritus “José Martí Pérez”. Cuba. Correo: oquero@uniss.edu.cu. ORCID ID: http://orcid.org/0000-0002-7872-2957. 2 Doctor
en Ciencias Pedagógicas. Profesor Auxiliar del departamento de Física-Matemática.
Universidad de Sancti Spíritus “José Martí Pérez”. Cuba. Correo: aldoruiz58@gmail.com . ORCID ID: https://orcid.org/0000-0003-1882-385X
______________________________________________________________
¿Cómo citar este artículo?
Quero
Méndez, O. N. y Ruiz Pérez, A. M. (Julio-octubre, 2021). La transferencia entre representaciones
verbales del plano en la formación de profesores de matemática. Pedagogía
y Sociedad, 24 (61), 300-324. Recuperado de http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/1238
______________________________________________________________
RESUMEN
Introducción: El
artículo propone la solución a un problema acerca de la transferencia entre
representaciones verbales del plano. Objetivo: exponer un procedimiento
didáctico dirigido a favorecer la transferencia entre representaciones verbales
del plano en el proceso de enseñanza- aprendizaje de la Geometría Analítica en
la formación de profesores de Matemática. Métodos
utilizados: histórico-lógico, analítico-sintético e inductivo-deductivo, para
el estudio de las fuentes de información y extraer de ellas regularidades
relacionadas con las representaciones y la transferencia entre estas; el
análisis de los productos del proceso pedagógico, la observación, las pruebas
pedagógicas y el análisis de tablas de frecuencias para valorar el aprendizaje. Resultados: los
principales aspectos de aprendizaje logrados con la aplicación del
procedimiento son: la identificación del tipo y la forma de la representación
dada y la representación buscada, conocimiento de los pasos del procedimiento y
la ejecución del procedimiento, aunque también se identificaron dificultades. Conclusiones:
el procedimiento propuesto incluye las acciones fundamentales dirigidas a la
planificación y la dinámica del proceso de enseñanza y aprendizaje de este
contenido. Los resultados en la medición del desempeño de los estudiantes donde
se implementó experimentalmente el procedimiento didáctico demuestran la
efectividad de este procedimiento.
Palabras clave: didáctica de la matemática;
docentes de matemática; formación de docentes; transferencia
entre representaciones verbales
del plano
______________________________ABSTRACT
The article proposes the solution to a
problem about the transference between verbal representations of the plane. Objective:
to present a didactic procedure aimed at favoring the transference between
verbal representations of the plane in the teaching-learning process of
Analytical Geometry in the training of mathematics professors. Methods:
historical-logical, analytical-synthetic and inductive-deductive were used for
the study of information sources and for the identification of regularities
related to representations and the transference between them, as well as the
analysis of the aspects of the pedagogical process, the observation, the
pedagogical tests and the analysis of frequency tables to assess learning. Results:
The identification of the type and form of the given representation and the sought
representation; the different steps of the procedure and its application;
although some encountered difficulties, too. Conclusion: the proposed
procedure includes the fundamental actions directed to the planning and
dynamics of the teaching/learning process of this content. The obtained results
from the measurement of the performance of the students involved in the
experimental implementation of the didactic procedure demonstrate its effectiveness.
Keywords:
training of Mathematics professors; didactic procedure; transference between
verbal representations of the plane.
INTRODUCCIÓN
l
papel del trabajo con representaciones de los objetos matemáticos es un tema
que ha acaparado la atención de investigadores en didáctica de la Matemática
desde la década de los 70 del pasado siglo. Los inicios del interés por este
tema se remontan a la tesis doctoral de Claude Janvier (1978) sobre el
aprendizaje de las funciones.
Las
ideas de la tesis de Janvier, fueron perfeccionadas posteriormente por el
propio Janvier y otros investigadores del Shell Center for Mathematical
Education. En 1987 Janvier publicó el libro titulado Problems of
Representation in the Teaching and Learning of Mathematics en el que se
extienden estas ideas a otros objetos matemáticos.
La
obra de Janvier se divulgó en Europa y otros países del mundo y en varios de
ellos los investigadores en didáctica de la Matemática, el profesorado de la
asignatura e instituciones se interesaron por el papel de las representaciones
en el aprendizaje de la Matemática. Así surgieron otros líderes científicos que
desarrollaron la teoría y elaboraron propuestas para aplicarla.
Por
esta razón esta tendencia didáctica ha tenido un gran impacto internacional,
tanto en la práctica como en la investigación. Prueba de ello es que en la base
teórica de proyectos internacionales importantes sobre evaluación de la calidad
de la educación como PISA y Timss se incluye el trabajo con representaciones.
En la base teórica de Timss se señala: “La representación de ideas crea el
núcleo del pensamiento matemático y de la comunicación, y la capacidad para
crear representaciones equivalentes es fundamental para conseguir el éxito en
la asignatura” (como se citó en Mullis y Martin, 2020, p. 25).
Otro
factor que ha contribuido a la globalización del trabajo con representaciones
en el proceso de enseñanza-aprendizaje (PEA) de la Matemática es su inclusión
en los Principios y Estándares del Consejo Nacional de Profesores de Matemática
de los Estados Unidos de América (NCTM). En la última versión de este documento
(año 2000), la representación es el segundo de los cinco procesos matemáticos
reconocidos (National Council of Teachers of Mathematics /NCTM/, 2000).
La
investigación sobre el trabajo con representaciones mantiene su actualidad a
nivel internacional: en la base de datos ERIC se registran 799 publicaciones
sobre este tema en 2020 y 17446 desde 1999 hasta la fecha, las cuales cubren
todos los niveles de educación.
Algunos
de los trabajos más recientes corresponden a Ospina (2012), Amaya y Medina
(2013), Amaya, Pino Fan y Medina (2016) y Meza y Amaya (2017) todos relativos
a las representaciones en el estudio de las funciones.
En
Cuba ha sido pobre la influencia de los trabajos de Janvier y de la comunidad
que investigaba sobre el papel de las representaciones en el PEA de la
Matemática en el siglo XX.
El Ministerio
de Educación (Mined) en los últimos años ha asumido las tendencias
internacionales sobre la enseñanza y aprendizaje de la Matemática y las ha
incluido en los documentos metodológicos y libros de texto. Respecto al trabajo
con representaciones en el cuarto de los lineamientos correspondientes al
enfoque metodológico general de la asignatura Matemática se plantea: “Propiciar la reflexión, el análisis de los
significados y formas de representación de los contenidos, el establecimiento
de sus relaciones mutuas, (…)” (Álvarez, Almeida y Villegas, 2014, p. 2).
En
correspondencia con este lineamiento se ha incluido el trabajo con
representaciones de objetos matemáticos en la línea directriz “Adiestramiento
lógico-lingüístico” (Álvarez, Almeida y Villegas, 2014).
En
Cuba la investigación sobre el trabajo con representaciones es escasa e
incipiente. En la revisión bibliográfica realizada por Quero durante su
investigación doctoral (Quero, 2018) acerca de la transferencia entre
representaciones de objetos de la Geometría Analítica en la formación de
profesores de Matemática se identificaron solo una tesis de doctorado (Gómez,
2005) y dos de maestría sobre el tema (Cañizares, 2010; Leyva, 2012); las tres
enmarcadas en las funciones, dos en la Educación Preuniversitaria y una en la
Educación Superior.
El
trabajo con representaciones en el PEA de la Geometría Analítica
correspondiente a la formación de profesores de Matemática generalmente
transcurre espontáneamente, según la lógica de la exposición del contenido
matemático tal cual aparece en los libros, sin prestársele mucha atención al
papel de la asignatura en la formación didáctica. En lo que respecta a la
transferencia entre representaciones de objetos de la Geometría Analítica
(Teroga) y particularmente del plano se presta poca atención al tratamiento de
todos los casos que se pueden presentar, y quedan varios de ellos sin incluir
en el contenido de la asignatura, entre los cuales están los relativos a las
transferencias entre representaciones verbales.
Son
posibles causas de esta situación problemática el insuficiente desarrollo de la
teoría de la representación de los objetos geométricos y las carencias de la
bibliografía que se utiliza en el PEA de la asignatura, consistentes en que en
ella no se exponen todas las transferencias posibles, no se describen los
procedimientos a utilizar en la transferencia entre representaciones verbales y
la ausencia de ejercicios y problemas dirigidos a la elaboración y fijación de
procedimientos.
El
artículo ofrece respuesta a las insuficiencias y carencias señaladas, pues
contiene contribuciones de los autores a la teoría de las representaciones de
objetos de la Geometría Analítica en el PEA, un procedimiento didáctico para la
transferencia entre representaciones verbales del plano en la formación de
profesores de Matemática y el análisis de los resultados de su aplicación. Su objetivo
es exponer un procedimiento didáctico dirigido a favorecer la transferencia
entre representaciones verbales del plano en el proceso de enseñanza-
aprendizaje de la Geometría Analítica en la formación de
profesores de Matemática
MARCO
TEÓRICO O REFERENTES CONCEPTUALES
Los
conceptos de representación y transferencia entre representaciones
Las
definiciones de los conceptos de representación de un plano, tipo de
representación de un plano, representación verbal de un plano, forma de
representación de un plano, forma reconocida de representación de un plano y
transferencia entre representaciones de un plano y sus conceptos subordinados
que se exponen a continuación, así como las notaciones utilizadas han resultado
de la particularización de las definiciones y notaciones introducidas por los
autores referidas a un objeto de la Geometría Analítica (Quero y Ruiz, 2018).
Se
entiende por representación de un plano (objeto representado) el objeto
material o mental (objeto representante) que lo sustituye y lo hace presente
determinándolo de forma única en el pensamiento, el lenguaje y la comunicación
con el uso de un sistema de coordenadas elegido convenientemente como sistema
de referencia.
Para
denotar las representaciones de un plano, los sistemas de coordenadas
utilizados como sistemas de referencia y los tipos de estos sistemas de
coordenadas se utilizan, respectivamente, las letras latinas R y C y la letra
griega minúscula t; todas seguidas de un subíndice. Los
sistemas de coordenadas pueden ser de tipo cartesiano, cilíndrico y esférico.
Los
tipos de representaciones del plano son subclases de la extensión de este
concepto cuyo estudio tiene un interés especial y se denotan con la letra T
seguida de un subíndice. Los de mayor interés en el PEA de la Geometría
Analítica son los tipos verbal, gráfico y analítico; en este artículo se
utiliza el tipo verbal.
Representación
verbal de un plano, en la Geometría Analítica, es una representación
mediante una frase que está compuesta por palabras del lenguaje común, palabras
de la terminología matemática y eventualmente por signos matemáticos,
particularmente de la Geometría Analítica. Por ejemplo, la frase: “plano que
pasa por los puntos A(3;-1;2), B(4,-1;-1) y C(2;0;2)” es una representación de
este tipo.
Toda
representación verbal de un plano está basada en entes que lo determinan con
unicidad como son, por ejemplo: tres de sus puntos no alineados, dos rectas que
se cortan, un punto y una recta que no pasa por este punto, dos rectas
paralelas (distintas) y, un punto del plano y dos vectores linealmente
independientes paralelos al plano.
Además
del concepto de tipo de representación, se utiliza como herramienta teórica el
concepto de forma de representación de un plano, entendida como la
configuración general del objeto representante, de modo que dos
representaciones de diferentes tipos tienen distintas formas, mientras que dos
representaciones del mismo tipo pueden tener la misma forma o formas distintas.
Las formas de representación de un plano se denotan con la letra F seguida de
un subíndice.
Las
siguientes son representaciones verbales de un plano α con formas
diferentes. En la primera de ellas el plano está determinado por tres puntos
no alineados y en la segunda, por un punto del plano y dos vectores paralelos a
él:
§ Plano
que pasa por los puntos A(3;4;-5) , B(6;5,-6) y C(4,2;-4).
§ Plano
que pasa por el punto A(3;4;-5) y es paralelo a los vectores a=(3;1,-1) y
b=(1;2;-1).
Como
el conocimiento matemático se construye en el marco de una institución, las
formas de representación de un plano aceptadas en la institución matemática se
llaman formas reconocidas de representación.
La
transferencia entre representaciones es uno de los procesos involucrados en el
trabajo con representaciones. En las fuentes bibliográficas consultadas se
trata con distintos nombres, entre ellos, traducción (Rico, 2009), conversión o
tratamiento (Duval, 2006, 2016) y juego de marcos (Douady, 2000).
La
idea esencial de la transferencia entre dos representaciones de un objeto
geométrico O considera que para O existen dos representaciones R1 y
R2, de las cuales una es conocida y la otra desconocida.
El
proceso que consiste en obtener la representación desconocida a partir de la
conocida se llama transferencia entre esas dos representaciones. Por ejemplo,
se sabe que para todo plano existe un sistema de ecuaciones paramétricas
(representación R1) y una ecuación general (representación R2).
Si para un plano particular se conociera su ecuación general y se desconociera
su sistema de ecuaciones paramétricas, el proceso mediante el cual se obtiene
el sistema de ecuaciones paramétricas a partir de la ecuación general es la
transferencia de R2 a R1.
Para
perfeccionar la idea anterior los autores de este escrito consideraron, además,
las formas respectivas F1 y F2 de las representaciones R1
y R2, los respectivos tipos T1 y T2 de
estas representaciones, los sistemas de coordenadas C1 y C2
utilizados en las representaciones R1 y R2 y los
respectivos tipos t1 y t2 de
estos sistemas de coordenadas. La definición resultante a partir de esta
consideración es la siguiente:
Si O
es un plano, determinado por su representación R1 en la forma F1
del tipo T1 correspondiente al sistema de coordenadas C1 de
tipo t1 y se
desconoce su representación R2 en la forma F2 del tipo T2
correspondiente al sistema de coordenadas C2 de tipo t2, el
proceso mediante el cual se obtiene R2 a partir de R1 se
llama transferencia de R1 a R2. Si inversamente se
conociera R2 y desconociera R1, el proceso que permite
obtener R1 a partir de R2 se llama transferencia de R2
a R1.
Cuando
C1=C2 la transferencia se llama transferencia intrasistema,
si en cambio C1≠C2, esta se denomina transferencia intersistemas.
Cuando T1=T2 la transferencia se llama transferencia intratipo,
si en cambio T1≠T2, esta recibe el nombre de
transferencia intertipos. Si quien realiza la transferencia de R1
a R2 o de R2 a R1 no utiliza una tercera
representación reconocida del objeto O como representación intermedia, la
transferencia se llama directa. En otro caso la transferencia se llama compuesta.
Una
transferencia entre representaciones de un objeto O será directa o compuesta en
dependencia del desarrollo del sistema de representación y del procedimiento
utilizado por el sujeto que la realiza.
El
análisis del factor referido a los medios para realizar la transferencia
conduce a diferenciar las transferencias que se realizan en la forma
tradicional con lápiz y papel de las que se realizan con el uso de algún
software. Es por eso que se consideran dos tipos de transferencia, según los
medios utilizados: transferencia con lápiz y papel y transferencia con
el uso de un software.
La
transferencia entre dos representaciones del plano en la Geometría Analítica es
un proceso que requiere de la aplicación de un procedimiento que garantice la
obtención de una representación procedimiento que garantice la obtención de una
representación desconocida a partir de una conocida. A la primera se le llama
representación dada (RD) y a la segunda, representación buscada (RB).
Procedimiento
para favorecer la transferencia entre representaciones verbales del plano
El
procedimiento está compuesto por seis acciones y perfecciona y amplía el
expuesto en Quero y Ruiz (2016). Las acciones son:
1) Determinación
de las formas de representación verbales del plano
Las
principales representaciones verbales de un plano en el PEA de la Geometría Analítica
en la formación de profesores de Matemática corresponden a las formas: 1) frase
con tres puntos no alineados, 2) frase con un punto del plano y un vector
normal, 3) frase con un punto del plano y dos vectores de dirección, 4) frase
con un punto del plano y una recta que no pasa por el punto, 5) frase con dos
rectas que se cortan y 6) frase con dos rectas paralelas diferentes.
2) Determinación
de las posibles transferencias entre representaciones verbales del plano
Para
el plano se han considerado seis formas de representación verbal, cada
transferencia entre representaciones con alguna de estas formas se puede
modelar con el concepto de par ordenado en que no pueden repetirse sus
componentes. Por esta razón es aplicable la regla del producto de la
combinatoria. Para la representación dada son posibles seis opciones, puesto
que no se puede repetir las componentes, después de elegida cada una de estas
opciones para la representación buscada son posibles cinco opciones. Al
multiplicar seis por cinco se obtienen 30 casos posibles para las
transferencias entre representaciones del tipo verbal.
La
transferencia entre representaciones se puede representar simbólicamente
utilizando una flecha y dos etiquetas (Tabla 1).
Tabla 1: Casos posibles de transferencia
entre representaciones verbales
|
|
Transferencias a
partir de la representación dada
|
Plano representado
utilizando tres puntos (TP)
|
1) TP→PVD, 2)
TP→PVN, 3) TP→PR,
4) TP→RRC y
5) TP→RRP
|
Plano representado
por un punto y dos vectores de dirección (PVD).
|
6) PVD→TP, 7)
PVD→PVN, 8) PVD→PR, 9) PVD→RRC y 10)PVD→PRP
|
Plano representado por
un punto y un vector perpendicular (PVN)
|
11) PVN→TP, 12) PVN→PVD, 13)
PVN→PR, 14) PVN→RRC y 15) PVN→RRP
|
Plano representado
por un punto y una recta que no pasa por el punto (PR)
|
16) PR→TP, 17) PR→PVD, 18)
PR→PVN, 19) PR→RRC y 20) PR→RRP
|
Plano representado
por dos rectas que se cortan (RRC)
|
21) RRC→TP, 22)
RRC→PVD, 23) RRC→PVN, 24) RRC→PR y 25) RRC→RRP
|
Plano representado
por dos rectas paralelas (RRP)
|
26) RRP→TP, 27)
RRP→PVD, 28) RRP→PVN, 29) RRP→PR y 30)
RRP→RRC
|
Fuente:
Elaboración propia
3) Elaboración
de tareas de aprendizaje para las transferencias
Después de identificar las posibles
transferencias a realizar se necesita elaborar las tareas de aprendizaje para
la elaboración y fijación de procedimientos de transferencia. Las variables de
tarea a tener en cuenta son: 1) tipo de transferencia a realizar, 2)
estructura de la tarea según su exigencia y 3) conocimiento del procedimiento
por el estudiante procedimientos de transferencia.
Las
variables de tarea a tener en cuenta son: 1) tipo de transferencia a realizar,
2) estructura de la tarea según su exigencia y 3) conocimiento del
procedimiento aquí por el estudiante. La primera variable puede tomar los
valores: transferencia directa con lápiz y papel (1.1), transferencia compuesta
con lápiz y papel (1.2) o transferencia
compuesta con software (1.3). La segunda puede tomar los valores: tarea de
respuesta abierta (2.1) o tarea de
completamiento (2.2) y la tercera: el estudiante conoce el procedimiento (3.1)
y el estudiante no conoce el procedimiento (3.2). Aplicando el principio de
multiplicación de la teoría combinatoria se obtienen 12 tipos de tareas (Tabla
2).
|
Tabla 2: Tipos de tareas de
aprendizaje que exigen transferencia
|
|
Tipo
|
Valor de la variable 1
|
Valor de la variable 2
|
Valor de la variable 3
|
|
1
|
1.1
|
2.1
|
3.1
|
|
2
|
1.1
|
2.1
|
3.2
|
|
3
|
1.1
|
2.2
|
3.1
|
|
4
|
1.1
|
2.2
|
3.2
|
|
5
|
1.2
|
2.1
|
3.1
|
|
6
|
1.2
|
2.1
|
3.2
|
|
7
|
1.2
|
2.2
|
3.1
|
|
8
|
1.2
|
2.2
|
3.2
|
|
9
|
1.3
|
2.1
|
3.1
|
|
10
|
1.3
|
2.1
|
3.2
|
|
11
|
1.3
|
2.2
|
3.1
|
|
12
|
1.3
|
2.2
|
3.2
|
Fuente:
Elaboración propia
Ejemplos
de tareas son los siguientes:
Ejemplo
1.
El
plano a pasa por los puntos no
alineados P(1;4;-4), Q(2;5;3) y R(3;0;-2).
Obtenga
representaciones verbales de a determinadas por: 1) un punto y dos
vectores paralelos al plano, 2) un punto y un vector normal, 3) dos rectas
paralelas, 4) dos rectas que se cortan y 5) por un punto y una recta que no lo
contiene.
Ejemplo 2.
Un
plano e contiene las rectas paralelas r:  y s:
y s: 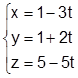
Obtenga
representaciones verbales de e determinadas por: 1)
tres puntos no alineados, 2) un punto y dos vectores paralelos al plano, 3) un
punto y un vector normal, 4) dos rectas que se cortan y 5) por un punto y una
recta que no lo contiene.
4) Proyección
de la utilización de las tareas en el PEA de la Geometría
Analítica
Para la
utilización de las tareas de aprendizaje en el PEA con el propósito de elaborar
o fijar los procedimientos de transferencia entre representaciones verbales del
plano es necesario:
§ Ordenar
las transferencias, atendiendo a su nivel de complejidad, para su uso en el
PEA.
§ Distribuir
las transferencias por formas organizativas (FO) del PEA (fundamentalmente la
clase y la autopreparación) y por tipos de clases (conferencias y clases
prácticas o encuentros). Se utilizó también el trabajo extraclase como tipo de
evaluación parcial (Tabla 3).
|
Tabla
3: Distribución de las transferencias entre representaciones en el PEA
|
|
Tipo
de actividad
|
Transferencias
|
|
Conferencias
|
1,
2, 6 y 11
|
|
Clases
prácticas
|
3,
4, 5, 8, 9, 10, 13, 14 y 15
|
|
Autopreparación
|
7,
12, 16, 17, 18, 19 y 20
|
|
Trabajo
extraclase
|
21,
22, 23, 24, 25, 26, 27, 28, 29 y 30
|
Fuente: Elaboración propia
§ Seleccionar
las tareas a realizar por los estudiantes en cada forma organizativa y tipo de
clase, así como las que deben resolver en trabajo extraclase.
§ Incluir
las tareas en la planificación de las actividades del PEA de la Geometría
Analítica.
5) Elaboración
y aplicación de procedimientos de transferencia
La
elaboración de procedimientos de transferencia requiere de la aplicación de un
programa heurístico particular donde se concreten las etapas y acciones del
programa heurístico general.
A
este programa los autores de este artículo lo han denominado Programa
Heurístico para la Transferencia entre Representaciones de Objetos de la
Geometría Analítica (PH-Teroga).
En
el PH-Teroga se inserta un sistema de preguntas con carácter heurístico (SPCH)
como un sistema de reglas o sugerencias heurísticas que favorecen la Teroga.
El
PH-Teroga se elabora en el estudio de la recta utilizando
tareas que exigen transferencia entre representaciones cuyo procedimiento de
transferencia no es conocido por los estudiantes.
Las
preguntas del SPCH contribuyen a la ejecución de las acciones principales del
PH-Teroga y se insertan en sus fases.
Las
fases fundamentales y acciones principales del PH-Teroga y el SPCH se exponen
en las tablas 4 y 5.
Entre
las fases de este programa existen relaciones sincrónicas y diacrónicas porque
unas preceden a las otras, pero también se entremezclan en su transcurso.
|
Tabla
4: Fases fundamentales y acciones principales del PH-Teroga
|
|
Fases
|
Acciones
principales
|
|
1.
Comprensión de la tarea de transferencia.
|
Reconocer que se trata de
un ejercicio o problema de transferencia.
Identificar la RD y la RB.
Identificar el tipo y la
forma de la RD y la RB.
Identificar el tipo de transferencia a realizar
(intrasistema o intersistemas, intratipo o intertipos).
Representar simbólicamente
la transferencia.
|
|
2.
Elaboración de un procedimiento de transferencia
|
Determinar los medios a
utilizar para realizar la transferencia.
Decidir si se puede
realizar una transferencia directa o es imprescindible realizar una
transferencia compuesta.
Elaborar un procedimiento
de transferencia.
Fundamentar el
procedimiento.
|
|
3.
Realización de la transferencia
|
Ejecutar el procedimiento
de transferencia.
Tomar decisiones
ejecutivas.
|
|
4.
Evaluación del proceso de transferencia
|
Comprobar si la
representación obtenida corresponde al objeto geométrico dado.
Determinar si la
representación obtenida es única o existen varias representaciones del mismo
objeto que satisfacen las exigencias de la tarea de aprendizaje.
Determinar si existen
otros procedimientos para realizar la transferencia.
Valorar si el
procedimiento aplicado se puede generalizar a todas las tareas del mismo tipo
que la resuelta.
Formular nuevos ejercicios
o problemas de transferencia.
|
Fuente: Tesis
doctoral Quero (2018, p.77)
|
Tabla 5: Preguntas con
carácter heurístico por fases del PH-Teroga
|
|
Fases
fundamentales
|
SPCH
|
|
1.
Comprensión de la tarea de transferencia
|
¿Cuál es el objeto
geométrico?
¿Se trata de una tarea de
transferencia entre representaciones de un objeto de la Geometría Analítica?
¿De qué tipo es la RD?
¿Qué forma tiene la RD?
¿Qué datos tengo de la RD?
¿De qué tipo es la RB?
¿Qué forma tiene la RB?
¿De qué tipo es la
transferencia a realizar?
|
|
2.
Selección o elaboración de un procedimiento para la
transferencia
|
¿Debo realizar la
transferencia con lápiz y papel o puedo utilizar un software?
¿Puedo pasar directamente
de la RD a la RB?
¿Es útil obtener una
representación intermedia?
¿Cómo puedo obtener la RB
a partir de la RD?
¿Cómo justifico el
procedimiento seguido?
|
|
|
|
|
3.
Realización de la transferencia
|
¿Qué hago para ejecutar
cada paso del procedimiento?
¿Qué utilidad tiene el
resultado parcial que obtengo al ejecutar cada paso?
|
|
4.
Evaluación del proceso de transferencia
|
¿Satisface la
representación obtenida las exigencias de la tarea? ¿Cómo lo puedo comprobar?
¿Es única la
representación obtenida?
¿Se pueden utilizar otros
medios para realizar la transferencia? ¿Cómo procedo si utilizo otros medios?
¿El procedimiento aplicado
se puede utilizar en todas las tareas del mismo tipo que la resuelta?
¿Existe otra forma de
proceder utilizando los mismos medios?
¿Qué nuevas tareas puedo
plantear a partir de la tarea resuelta?
|
Fuente:
Tesis doctoral Quero (2018, p.78)
La
elaboración de procedimientos de transferencia ocurre durante la resolución de
tareas de aprendizaje que exigen transferencia entre representaciones cuyos
procedimientos son desconocidos por el estudiante y la resolución de estas tareas
transcurre según las funciones didácticas.
La
aplicación de los procedimientos de transferencia debe tener lugar durante la
resolución de tareas que exigen transferencia entre representaciones verbales
del plano cuyos procedimientos el estudiante conoce y transcurre según las
funciones didácticas.
6) Evaluación
del desempeño
La
evaluación es uno de los eslabones del PEA y respecto a su ejecución son
importantes las respuestas a las preguntas ¿qué?, ¿cuándo y ¿cómo evaluar?
En
cuanto al ¿qué evaluar?, se deben atender cinco objetos interrelacionados: 1)
las condiciones previas necesarias para elaborar o aplicar un procedimiento de
transferencia entre representaciones verbales del plano, incluido el
conocimiento del PH-Teroga y del sistema de preguntas con carácter heurístico,
2) la habilidad para aplicar el PH-Teroga, 3) las habilidades para aplicar los
procedimientos de transferencia elaborados, 4) características de la esfera
afectivo-motivacional de la personalidad imbricadas en los objetos anteriores y
5) la comunicación a propósito de la transferencia entre representaciones.
La
evaluación de las condiciones previas necesarias para elaborar o aplicar un
procedimiento de transferencia entre representaciones verbales del plano forma
parte de la función didáctica de aseguramiento del nivel de partida.
La
habilidad para aplicar el PH-Teroga debe ser evaluada en la resolución de una
tarea que exige transferencia entre representaciones verbales del plano cuando
se desconoce el procedimiento de transferencia necesario, es decir, en tareas
del tipo 2, 4, 6, 8, 10 o 12 (Tabla 2).
Para
obtener datos que propicien hacer inferencias acerca del dominio de esta
habilidad, el profesor debe observar la actuación de sus estudiantes mientras
resuelven las tareas y de ser necesario ha de realizar un análisis de los
productos de la actividad ejecutada, a partir de la recogida de la libreta de
notas o de cualquier otro soporte, donde esté registrada la información
generada durante la resolución de las tareas.
La
evaluación de las habilidades para aplicar los procedimientos de transferencia
elaborados debe realizarse cuando se resuelven tareas que exigen un
procedimiento de transferencia conocido, es decir, tareas de los tipos 1, 3, 5,
7, 9 o 11 (Tabla 2). En ello el profesor puede utilizar los mismos métodos que
en la evaluación de la habilidad para aplicar el PH-Teroga.
En
la esfera afectivo-motivacional debe valorarse el interés por resolver las
tareas, la perseverancia ante la complejidad de las tareas, la actitud ante las
críticas de los demás y el estado de ánimo durante la resolución de las tareas.
Con
relación a la comunicación, debe evaluarse la comunicación con el profesor, la
comunicación con los compañeros de clase y la comunicación matemática oral
METODOLOGÍA EMPLEADA
Entre
los métodos utilizados en la investigación que originó el artículo se
encuentran el histórico-lógico, analítico-sintético y el inductivo-deductivo.
El
uso de estos métodos permitió identificar las principales tendencias cubanas e
internacionales acerca de las concepciones de los tres conceptos centrales de
la teoría de las representaciones de los objetos matemáticos: representación,
transferencia entre representaciones y sistema de representación. A partir de
una sistematización de estas tendencias los autores realizaron una
reconceptualización de estos tres conceptos para su uso en el PEA de la
Geometría Analítica e introdujeron los conceptos de tipo y forma de
representación en el sentido en que ellos son usados en este artículo.
El
procedimiento didáctico que se expone aquí está basado en los fundamentos
teóricos desarrollados por los autores. En este procedimiento se utiliza como
método matemático la regla del producto de la teoría combinatoria para la
determinación de las transferencias entre representaciones verbales del plano.
También se emplea este método para la determinación de los tipos de tareas a
partir de las variables de tareas consideradas.
Para
la medición del aprendizaje alcanzado acerca de la transferencia entre
representaciones verbales del plano se utilizaron como métodos el análisis de
los productos del proceso pedagógico, la observación, las pruebas pedagógicas y
el análisis de tablas de frecuencias.
RESULTADOS Y DISCUSIÓN
El
procedimiento didáctico expuesto en la sección anterior ha sido aplicado en el
proceso de enseñanza-aprendizaje de la Geometría Analítica en la formación de
profesores de Matemática en la Universidad de Sancti Spíritus “José Martí
Pérez”. En su elaboración se utilizó la evaluación En el pre-experimento se
utilizó como variable de estudio el desempeño de los estudiantes en la
transferencia entre representaciones verbales del plano, como unidad de estudio
el estudiante que se forma como profesor de Matemática en la licenciatura en
Educación, perfil Matemática, y como unidad de análisis la tarea que exige
transferencia entre representaciones verbales del plano. La
investigación se desarrolló con los 14 estudiantes del único grupo del tercer
año de la carrera
El
diseño de la medición de la variable de estudio se realizó según el
procedimiento propuesto por Ruiz (2006): 1) definición de la variable, 2)
determinación de las dimensiones y de los indicadores de cada dimensión, 3)
modelación de los indicadores mediante variables estadísticas, 4) establecimiento
de los criterios de medición de los indicadores y su representación en matrices
de valoración, 5) diseño de los instrumentos de medición y evaluación de su
validez y confiabilidad y 6) diseño de la medición de las dimensiones y de la
variable.
Las
dimensiones de la variable de estudio son: 1) dimensión
cognitivo-procedimental, 2) dimensión afectivo-motivacional y 3) dimensión
motivacional. En la dimensión cognitivo-procedimental se consideran dos
subdimensiones: 1.1) elaboración de procedimientos de transferencia y 1.2)
aplicación de procedimientos de transferencia. La primera subdimensión tiene
10 indicadores y la segunda seis (tablas 6 y 7).
Los
indicadores de la dimensión afectivo-motivacional son: 2.1)
interés por resolver las tareas, 2.2) perseverancia ante la complejidad de las
tareas, 2.3) actitud ante las críticas de los demás y 2.4) estado de ánimo
durante la resolución de las tareas.
Los
indicadores de la dimensión comunicacional son: 3.1) atención prestada a las
explicaciones del profesor, 3.2) actuación ante las interrogantes formuladas
por el profesor, 3.3) colaboración con los compañeros de clase, 3.4) atención
prestada a las explicaciones de los compañeros de clase, 3.5) actuación ante
las interrogantes formuladas por sus compañeros de clase y 3.6) utilización de
la terminología matemática.
A
cada indicador se le asoció una variable
estadística, cuya escala de medición está compuesta por las categorías: alto,
medio y bajo. Para la medición de los indicadores se utilizaron matrices de
valoración (López, 2020), que contienen los criterios utilizados.
Los
resultados obtenidos en la medición de los indicadores de la dimensión
cognitivo-procedimental a los 14 estudiantes que se forman como profesores de
Matemática se exponen en las tablas 6 y 7.
|
Tabla
6: Resultados de la medición de los indicadores de la subdimensión
“Elaboración de procedimientos de transferencia”
|
|
Indicador
|
Alto
|
%
|
Medio
|
%
|
Bajo
|
%
|
|
1.1.1)
Identificación del tipo y la forma de la RD y la RB
|
4
|
28,6
|
10
|
71,4
|
0
|
0
|
|
1.1.2)
Identificación del tipo de transferencia a realizar
|
3
|
21,4
|
10
|
71,4
|
1
|
7,1
|
|
1.1.3)
Elaboración de un procedimiento de transferencia
|
5
|
35,7
|
5
|
35,7
|
4
|
28,6
|
|
1.1.4)
Fundamentación del procedimiento
|
4
|
28,6
|
5
|
35,7
|
5
|
35,7
|
|
1.1.5)
Ejecución del procedimiento con lápiz y papel
|
5
|
35,7
|
5
|
35,7
|
4
|
28,6
|
|
1.1.6)
Ejecución del procedimiento con software
|
4
|
28,6
|
6
|
42,9
|
4
|
28,6
|
|
1.1.7)
Comprobación de si la representación obtenida corresponde al objeto
geométrico dado
|
1
|
7,2
|
8
|
57,1
|
5
|
35,7
|
|
1.1.8)
Determinación de si la representación obtenida es única
|
5
|
35,7
|
4
|
28,6
|
5
|
36
|
|
1.1.9)
Determinación de si existen otros procedimientos para realizar la
transferencia
|
5
|
35,7
|
3
|
21,4
|
6
|
42,9
|
|
1.1.10)
Formulación de nuevos ejercicios o problemas de transferencia
|
3
|
21,4
|
4
|
28,6
|
7
|
50,0
|
Fuente:
Elaboración propia
|
Tabla
7: Resultados de la medición de los indicadores de la subdimensión
“Aplicación de procedimientos de transferencia”
|
|
Indicador
|
Alto
|
%
|
Medio
|
%
|
Bajo
|
%
|
|
1.2.1)
Identificación del tipo y la forma de la RD y la RB
|
12
|
85,7
|
2
|
14,3
|
0
|
0
|
|
1.2.2)
Conocimiento de los pasos del procedimiento
|
10
|
71,4
|
4
|
28,6
|
0
|
0
|
|
1.2.3)
Ejecución del procedimiento con lápiz y papel
|
6
|
42,9
|
8
|
57,1
|
0
|
0
|
|
1.2.4)
Ejecución del procedimiento con software
|
6
|
42,9
|
5
|
35,7
|
3
|
21,4
|
|
1.2.5)
Comprobación de si la representación obtenida corresponde al objeto
geométrico dado
|
2
|
14,3
|
7
|
50,0
|
5
|
35,7
|
|
1.2.6)
Determinación de si la representación obtenida es única
|
5
|
35,7
|
5
|
35,7
|
4
|
28,6
|
Fuente:
Elaboración propia
En
la subdimensión “Elaboración de procedimientos de transferencia” los
indicadores con mayor frecuencia de las categorías alto o medio son:
§ Identificación
del tipo y la forma de la representación dada y la representación buscada.
§
Identificación
del tipo de transferencia a realizar.
Los
indicadores con menor frecuencia de las categorías alto o medio son:
§ Formulación
de nuevos ejercicios o problemas de transferencia; solo tres estudiantes en la
categoría alto. Siete estudiantes no formularon nuevos ejercicios
o lo hicieron de forma incorrecta.
§ Comprobación
de si la representación obtenida corresponde al objeto geométrico dado; solo un
estudiante en la categoría alto. Cinco estudiantes no comprobaron o no explicaron
correctamente.
Respecto
a la dimensión “Aplicación de procedimientos de transferencia”, los indicadores
con mayor frecuencia de las categorías alto o medio son:
§
Identificación
del tipo y la forma de la representación dada y la representación buscada.
§
Conocimiento
de los pasos del procedimiento.
§
Ejecución
del procedimiento con lápiz y papel.
Los
indicadores con menor frecuencia de las categorías alto o medio son:
§
Comprobación
de si la representación obtenida corresponde al objeto geométrico dado.
§
Determinación
de si la representación obtenida es única. Cuatro estudiantes no determinaron
si la representación es única.
Se
identificaron los errores cognitivos siguientes:
§
Subdeterminación
de la representación: utilización de representaciones verbales que no
determinan de forma única al plano.
§
Sobredeterminación
de la representación: inclusión de características del plano no necesarias en
su representación verbal.
§
Determinación
de una representación incompatible: representación de un plano que no le
corresponde a la representación dada.
§
Otros
errores, entre ellos errores de cálculo al determinar coordenadas de puntos que
satisfacen la ecuación del plano, al resolver sistemas de ecuaciones y al
operar con vectores.
Los
resultados obtenidos en la medición de los indicadores de la dimensión
afectivo-motivacional se exponen en la Tabla 8.
|
Tabla
8: Resultados de la medición de los indicadores de la dimensión
afectivo-motivacional
|
|
Indicador
|
Alto
|
%
|
Medio
|
%
|
Bajo
|
%
|
|
2.1)
Interés por resolver las tareas de las clases prácticas
|
7
|
50,0
|
5
|
35,7
|
2
|
14,3
|
|
2.2)
Perseverancia ante la complejidad de las tareas
|
5
|
35,7
|
6
|
42,9
|
3
|
21,4
|
|
2.3)
Actitud ante las críticas de los demás
|
5
|
35,7
|
8
|
57,1
|
1
|
7,2
|
|
2.4) Estado de ánimo durante
la resolución de las tareas
|
5
|
35,7
|
8
|
57,1
|
1
|
7,2
|
Fuente:
Elaboración propia
Los
indicadores con mayor frecuencia de las categorías alto o medio son:
§
Actitud
ante las críticas de los demás.
§
Estado de
ánimo durante la resolución de las tareas.
Los
resultados obtenidos en la medición de los indicadores de la dimensión
comunicacional se exponen en la Tabla 9.
|
Tabla
9: Resultados de la medición de los indicadores de la dimensión
comunicacional
|
|
Indicador
|
Alto
|
%
|
Medio
|
%
|
Bajo
|
%
|
|
3.1) Atención
prestada a las explicaciones del profesor
|
8
|
57,1
|
5
|
35,7
|
1
|
7,2
|
|
3.2) Actuación
ante las interrogantes formuladas por el profesor
|
4
|
28,6
|
6
|
42,8
|
4
|
28,6
|
|
3.3) Colaboración
con los compañeros de clase
|
5
|
35,7
|
7
|
50,0
|
2
|
14,3
|
|
3.4)
Atención prestada a las explicaciones de los compañeros de clase
|
6
|
42,9
|
6
|
42,9
|
2
|
14,3
|
|
3.5) Actuación ante las
interrogantes formuladas por sus compañeros de clase
|
8
|
57,1
|
4
|
28,6
|
2
|
14,3
|
|
3.6) Utilización de
la terminología matemática
|
4
|
28,6
|
6
|
42,9
|
4
|
28,6
|
Fuente:
Elaboración propia
El
indicador con mayor frecuencia de las categorías alto o medio es “Atención
prestada a las explicaciones del profesor” y el de menor frecuencia es
“Utilización de la terminología matemática” pues cuatro estudiantes cometieron
más de dos errores.
El
papel de las representaciones de los objetos matemáticos en el PEA de la
Matemática ha sido un tema de interés de los investigadores en didáctica de la
Matemática desde la década de los 70 del siglo XX, pero en Cuba se incorporó en
los lineamientos para el trabajo en la asignatura tardíamente en la segunda
década del siglo XXI y la investigación en este tema es escasa e incipiente y
se ha centrado en el tema de las funciones.
El
procedimiento didáctico para la transferencia entre representaciones verbales
del plano en la formación de profesores de Matemática propuesto por los autores
de este artículo incluye las acciones fundamentales dirigidas a la
planificación y la dinámica del PEA de este contenido.
Los
resultados en la medición del desempeño de los estudiantes que se forman como
profesores de Matemática en la transferencia entre representaciones verbales
del plano donde se implementó experimentalmente el procedimiento didáctico
propuesto, demuestra la efectividad de este procedimiento en la muestra
estudiada. A pesar de ello se observaron limitaciones para comprobar si la
representación obtenida corresponde al objeto geométrico dado, determinar si la
representación obtenida es única, formulación de nuevos ejercicios o problemas
de transferencia y en la utilización de la terminología matemática.
REFERENCIAS
BIBLIOGRÁFICAS
Álvarez, M., Almeida, B. y Villegas, E.
(2014). El proceso de enseñanza-aprendizaje
de la asignatura
Matemática. Documentos metodológicos. La
Habana, Cuba: Editorial Pueblo y Educación.
Amaya, T. y Medina, A. (2013).
Dificultades de los estudiantes de grado once al hacer transformaciones de
representaciones de una función con el registro figural como registro
principal. Educación Matemática, 25(2), 119-140. Recuperado de https://www.revista-educacion-matematica.org.mx/revista/volumen25-numero2.
Amaya, T., Pino Fan, L. y Medina, A.
(2016). Evaluación del conocimiento de futuros profesores de matemáticas sobre
las transformaciones de las representaciones de una función. Revista
Educación Matemática, 28(3), 111-144. Recuperado de https://www.revista-educacion-matematica.org.mx/revista/volumen28-numero3.
Cañizares, E. (2010). La formación y
desarrollo de la habilidad para transferir entre representaciones analíticas y
gráfica de funciones cuadráticas en estudiantes de décimo grado (Tesis de
maestría). Universidad de Ciencias Pedagógicas “Silverio Blanco Núñez”,
Sancti Spíritus, Cuba.
Douady, R. (2000). Juego de marcos y
dialéctica herramienta-objeto. En G. Castrillón (Ed.), Ingeniería didáctica
(pp. 171-177) [versión electrónica]. Santiago de Cali. Colombia.
Duval, R. (2006). Un tema crucial en la
educación matemática: La habilidad para cambiar el registro de representación. Gaceta
de la Real Sociedad Matemática Española, 9 (1), 143–168. Recuperado
de https://eudml.org/doc/44160
Duval, R. (2016). Un análisis cognitivo
de problemas de comprensión en el aprendizaje de las matemáticas. En R. Duval y
A. Sáenz Ludlow. Comprensión y aprendizaje en matemáticas: perspectivas
semióticas seleccionadas (pp.61- 94). Bogotá, Colombia: Universidad
Distrital “Francisco José de Caldas”. . Recuperado de https://die.udistrital.edu.co/publicaciones/comprension_y_aprendizaje_en_matematicas_perspectivas_semioticas_seleccionadas
Gómez, M. (2005). Una propuesta
didáctica para elevar los niveles de transferencia entre las distintas
representaciones de las funciones, en el nivel preuniversitario (Tesis de
doctorado). Instituto Superior Pedagógico “Enrique J. Varona”, La Habana, Cuba.
Janvier, C. (1978). The
interpretation of complex cartesian graphs representing situations: Studies
and teaching experiments (Tesis de doctorado).
University of Nottingham. Nottingham, United Kingdom.
Janvier, C. (Ed.) (1987). Problems
of representation in the teaching and learning of mathematics. Hillsdale,
New Jersey : Erlbaum.
Leyva, T. (2012). Propuesta didáctica
para elevar los niveles de transferencia entre las distintas representaciones
de las funciones reales de una variable real, en el tema de funciones en el
primer año de la Universidad de Ciencias Informáticas (Tesis de maestría).
Instituto Superior Politécnico “José Antonio Echeverría”. La Habana, Cuba.
López, J. C. (2020). Rúbricas,
evaluación más allá de la calificación. Edukafé, Documentos de Trabajo de la
Escuela, (9). Recuperado de http://eduteka.icesi.edu.co/articulos/rubricas
Meza, F. y Amaya, T. (2017). Conflictos
epistémicos al hacer transformaciones en las representaciones de una función. Revista
Entornos, 29(1), 43-53. Recuperado de https://journalusco.edu.co/index.php/entornos.
Mullis, A., Martin, M. (2020).
Timss 2019. Marcos de la Evaluación. Madrid,
España: Instituto Nacional de Calidad y Evaluación. Recuperado de https://sede.educacion.gob.es/publiventa/descarga.action?f_codigo_agc=21779
National Council of Teachers
of Mathematics [NCTM] (2000). Principles and Standars for School Mathematic.
Reston,
Viginia: Autor.
Ospina, D. (2012). Las
representaciones semióticas en el aprendizaje del concepto función lineal
(Tesis de maestría). Universidad autónoma de Manizales, Colombia. Recuperado de
http://repositorio.autonoma.edu.co/jspui/bitstream/11182/245/1/Tesis
Quero, O. (2018). La transferencia
entre representaciones en el proceso de enseñanza-aprendizaje de la Geometría
Analítica en la formación inicial de profesores de Matemática (Tesis de
doctorado). Universidad de Sancti Spíritus “José Martí Pérez”, Sancti Spíritus,
Cuba.
Quero, O. y Ruiz, A. (2016).
Transferencias entre representaciones verbales de las secciones cónicas en la
formación del profesor de Matemática. Pedagogía y Sociedad, 19 (47),
19-37. Recuperado de http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/499.
Quero, O. y Ruiz, A. (2018).
Determinación de procedimientos de transferencia entre representaciones en el
proceso de enseñanza y aprendizaje de la Geometría Analítica. Unión, 52,
118-143. Recuperado de http://www.fisem.org/www/union/revistas/2018/52/05.pdf
Rico, L. (2009). Sobre las nociones de
representación y comprensión en la investigación en Educación Matemática. PNA,
Revista
de Investigación en Didáctica de la Matemática 4(1),
1-14.
Ruiz, A. (2006). Procedimientos y medios
para relacionar constructos, dimensiones, indicadores y medición en la
investigación pedagógica (curso post-evento). En A. Chinea, J. Medina e I.
Cabezas (Eds.). Actas del Evento Provincial Pedagogía 2007 (pp. 50-78).
Instituto Superior Pedagógico “Silverio Blanco”. Sancti Spíritus, Cuba:
Órgano Editor Educación Cubana.