RESUMEN
Introducción: El
rendimiento de los estudiantes del Curso por Encuentros en la Universidad de
Sancti Spíritus está afectado por altos niveles de desaprobados en el 1er año
de las carreras. Se puede lograr que aumenten los aprobados, si sus estrategias
de aprendizaje contribuyen a elevar el nivel de independencia cognoscitiva. Objetivo:
aplicar
una colección de problemas para mejorar la independencia cognoscitiva de los
estudiantes de primer año del Curso por Encuentros en el Centro Universitario
de Fomento, a través de la labor educativa en la asignatura Matemática. Métodos:
se
utilizó el método dialéctico materialista, y los métodos: histórico-lógico, analítico–sintético
y los del nivel empírico: observación pedagógica, prueba pedagógica y el
análisis documental.
Resultados: la
propuesta de solución presentada responde a una de las Líneas de Trabajo
Metodológico desarrolladas dentro de la universidad: “La
dirección del aprendizaje para el desarrollo de la independencia cognoscitiva
de los estudiantes desde la clase encuentro”, la cual contribuyó a
mejorar la independencia cognoscitiva de los estudiantes universitarios de 1er
año. Conclusiones: la
integración de acciones desde la clase encuentro en la asignatura Matemática del
1er año, ha permitido que los estudiantes universitarios mejoren sus
estrategias de aprendizaje, lo cual ha favorecido el desarrollo de su independencia
cognoscitiva.
Palabras clave: trabajo educativo; dirección
del aprendizaje; estudiantes universitarios; independencia cognoscitiva; matemática.
Introduction:
The performance of students from the part-time courses at the University of
Sancti Spíritus is impaired by elevated levels of students who fail subjects in
the first year of the different degree courses. The number of students passing
their exams can increase if their learning strategies contribute to raise the
level of cognitive independence. Objective: To
apply the proposal of a set of problems to improve the cognitive independence
of first year students from the part-time courses at the Fomento University
Center, through the educational work in Mathematics. Methods: The dialectical-materialistic, historical-logical
and analytic-synthetical methods were used, as well as the pedagogical
observation and tests and the analysis of documents from the empirical level. Results: The proposal is in line with one
of the methodological aspects dealt with at the university: “Directing the
learning process for the development of the cognitive independence in students
from the part-time courses” which contributed to improve the cognitive
independence of first year university students. Conclusions:
The set of tasks implemented in the subject of Mathematics in the
first year has allowed students to improve their learning strategies, thus
favoring the development of cognitive independence.
Keywords:
educational work; directing the learning
process; university students; cognitive independence; Mathematics;
INTRODUCCIÓN
on
el inicio de la vida universitaria, tiene que producirse en el estudiante una
ruptura cualitativa con su propio pasado, un cambio en su proceder, en su
actitud ante la vida y asumir muchas responsabilidades, este cambio se produce
también, en el plano intelectual, favoreciendo la independencia cognoscitiva
como rasgo esencial de la personalidad y cualidad principal de todo ser humano
que se forma mediante la actividad propia.
La
independencia cognoscitiva se ha estudiado desde diferentes posiciones teóricas
por varios autores entre ellos: Álvarez de Zayas (1998), Varela (2009), Díaz
(2011), Hernández, Cáceres, Barba y Losada (2016), Martínez, Valdés y Pérez
(2017), Rodríguez (2017) y Díaz (2017).
Con
el desarrollo científico-técnico que se aprecia en todas las esferas y en
especial en la enseñanza, se impone una nueva concepción de actividades
docentes y modos de aprender que coadyuven al desarrollo de la independencia
cognoscitiva del estudiante. La Matemática y dentro de ella la resolución de
problemas es un pilar esencial en la educación de las nuevas generaciones, el
importante papel desempeñado por esta asignatura en el desarrollo de la ciencia
y la tecnología hacen de su aprendizaje una necesidad para que los jóvenes
universitarios puedan recibir una preparación adecuada para la vida, la
profesión y la sociedad.
Los
estudiantes de 1er año de las diferentes carreras, en el Centro Universitario
de Fomento, tienen dificultades con su independencia cognoscitiva como parte de
su formación integral, pues no tienen una formación adecuada de las
habilidades para el trabajo independiente. Teniendo en cuenta el enfoque
metodológico que se da a los contenidos en la asignatura Matemática, esta problemática
aparece reflejada en su diagnóstico.
La importancia
del estudio realizado se fundamenta en que, en cada problema, se aprovechan las
vivencias de los estudiantes y se sugiere realizar pequeñas investigaciones,
convirtiendo así a los problemas en un reflejo de la realidad que motiva a
interactuar con los medios tecnológicos de la informática y las
telecomunicaciones para buscar el conocimiento necesario. Además, se contribuye
al desarrollo de habilidades para la búsqueda del conocimiento, al desarrollo
del pensamiento lógico, a la motivación por aprender y por lo tanto al logro
de la independencia cognoscitiva.
El objetivo de este artículo es: Aplicar
una colección de problemas para mejorar la independencia cognoscitiva de los
estudiantes de primer año del Curso por Encuentros en el Centro Universitario
de Fomento, a través de la labor educativa en la asignatura Matemática.
MARCO TEÓRICO O REFERENTES CONCEPTUALES
La
independencia cognoscitiva
El estudio sobre el tema de
la independencia cognoscitiva llevó a los autores a sistematizar los referentes
de varios autores, Zilberstein (2009) aconseja que el cambio de un proceso de
enseñanza aprendizaje tradicional, con énfasis en el componente instructivo,
educativo y desarrollador, generador de una actitud intelectual activa en el
alumno, precisa de la concientización por el docente de la necesidad del
cambio y de preparase para lograrlo, además Quero y Ruiz (2016) consideran que
las tareas de aprendizaje son de gran importancia en la fijación de los
procedimientos de transferencia que comienzan en el trabajo independiente
previo a cada clase, continúa en la clase y se extiende al trabajo
independiente posterior; así mismo, Martínez, Valdés y Pérez (2017) consideran
que la Matemática contribuye al desarrollo de capacidades mentales generales,
en la formación de conceptos, capacidades y habilidades y que los estudiantes
deben tener un pensamiento lógico desarrollado, saber operar de manera
independiente y aplicar los conocimientos matemáticos a diferentes situaciones
fuera de la Matemática. Estas opiniones muestran las potencialidades
que brindan los programas de las asignaturas para entrenar a los estudiantes en
habilidades para el estudio independiente, que les permita desarrollar o
fortalecer el funcionamiento eficaz de la independencia cognoscitiva.
¿Qué es la independencia cognoscitiva? Varios
son los autores que responden a la interrogante. La independencia
cognoscitiva se aborda desde diferentes posiciones teóricas, Rodríguez (2017)
considera que:
La
independencia cognoscitiva es actuar de forma autónoma, con criterios y
decisiones científicas que le permiten desarrollar modos de actuación propios,
que logra la búsqueda independiente de los conocimientos necesarios para su
actuación y actualización profesional, además es saber trabajar de forma
individual y en grupos, adquirir valores como responsabilidad, compañerismo y
solidaridad, entre otros, en esta la bien llamada era del conocimiento y de la información.
(pp. 2-3).
Varela (2009) razona que en
una época de constantes cambios y vastedad de información, la enseñanza en la
Educación Superior debe promover un modo de actuación con independencia
cognoscitiva evidenciado por saber realizar actividades relacionadas con la
búsqueda del conocimiento, que desarrolle habilidades como teorizar, crear
nuevas ideas, reflexionar, aplicar lo aprendido a nuevas situaciones y
resolver problemas relacionados con el perfil de su carrera. Los estudiantes
requieren ser activos, tener una motivación intrínseca y actuar sin niveles de
ayuda para alcanzar eficazmente sus metas en la vida.
Ambos puntos de vista, consideran la
independencia cognoscitiva como un modo de actuación que permite al estudiante
alcanzar sus metas, ser un egresado con criterios y decisiones científicas
propias. Además, les permite trabajar de manera individual o en equipo e
incentiva la formación de valores. Permite a los estudiantes resolver
problemas o formularlos por sí mismos, se entiende como una capacidad que está
estrechamente relacionada con el desarrollo de las capacidades creadoras de las
personas y que depende de otras capacidades.
Álvarez de Zayas (1998), ofrece su punto de
vista acerca de cómo se manifiesta la independencia cognoscitiva, asumida y
compartida por los autores de este artículo, al respecto señala:
La
independencia cognoscitiva se manifiesta en la capacidad de ver y de
representarse el problema, la tarea cognoscitiva de carácter
teórica o práctica; en la determinación del plan, los métodos para su
solución, utilizando los procedimientos más seguros y
efectivos; en el proceso mental activo, en la búsqueda creadora de soluciones
adecuadas; y en la comprobación de las soluciones adoptadas. (p. 50).
Por las opiniones del referido autor se puede
concluir que dentro del proceso docente, al estudiante, se le presentan
oportunidades para mejorar la forma de aprender y para incrementar el sistema
de conocimientos que posee, entre ellas están las guías de estudio
independiente que proponen los profesores después de cada clase; este es un recurso
didáctico idóneo para desarrollar la independencia cognoscitiva.
Sobre
la necesidad de independencia en el aprendizaje, el profesor de matemática Díaz
(2017) expresó que:
La
constante renovación tecnológica en los procesos productivos y el caudal de
información científica y técnica que necesita asimilar un obrero, un técnico o
un profesional para no quedar rezagados, les exigen haber desarrollado la
capacidad de orientarse por sus propios medios en esas fuentes de información
y aplicar esa información en la labor que cada uno de ellos lleva a cabo.
(p. VII).
Para tener mejores resultado
en la independencia cognoscitiva es prudente explorar las percepciones de los
estudiantes sobre sus docentes, donde den testimonio de lo que consideran
prácticas docentes innovadoras, flexibles, no rutinarias, que permiten el
aprender por sí mismos y que utilizan el pensamiento heurístico. En un reciente
artículo, los investigadores Zavala, González y Castro (2019) expresaron al
respecto que:
…se puede percibir que los estudiantes aunque no ubican
los términos correctos, se refieren a la función del docente respecto a la
metodología de enseñanza pues para ellos un docente innovador es aquel
dinámico y cambiante que les transmite la motivación por aprender, aquel
docente creativo y de mente abierta que acepta las opiniones tanto positivas
como negativas de los estudiantes con el fin de tomarlas como críticas
constructivas y mejorar en su práctica. (p. 15).
Los investigadores universitarios Hernández,
Cáceres, Barba y Losada (2016) en su participación en el evento nacional
Universidad 2016, presentaron un estudio
relacionado con la formación de profesionales universitarios y su independencia
cognoscitiva, desde el cual se manifestó que:
La
universidad del siglo XXI enfrenta importantes desafíos, entre ellos
reafirmarse como el espacio por excelencia de la educación superior, cuyo
propósito es la formación de profesionales idóneos y éticos, capaces de
promover no solo una sociedad competitiva, sino también participativa, justa y
democrática.( p. 3).
Durante el desarrollo del aprendizaje en las
universidades, en la modalidad semipresencial, es de gran importancia que el
estudiante tenga habilidades para adquirir conocimientos mediante el trabajo
independiente con el uso de libros de textos, software educativo,
enciclopedias, aulas virtuales, visualización de vídeos, etc. En la metodología
de la clase encuentro, el tiempo que el estudiante dedique al trabajo
independiente es determinante para el aprendizaje y por tanto para mejorar su
independencia cognoscitiva.
Hernández et al.
(2016), en su estudio sobre la independencia cognoscitiva, establecieron como
indicadores los siguientes:
· Utilización de estrategias
cognitivas para el aprendizaje.
· Formulación de hipótesis
relacionadas con las tareas docentes.
· Formulación de conclusiones.
· Utilización de los conocimientos
precedentes en la solución de los problemas docentes.
· Análisis de gráficos, esquemas,
modelos y figuras tridimensionales de manera independiente.
· Comunicación interactiva e
interés cognitivo.
· Disposición para solucionar los problemas docentes. (p. 8).
La investigadora Díaz (2011),
en su tesis de maestría, profundizó en el estudio de cómo contribuir a la
independencia cognoscitiva en escolares de sexto grado de la Educación Primaria
y trabajó con las siguientes dimensiones e indicadores:
Dimensión 1. Esfuerzo
personal.
- Se manifiestan constantes
en la solución de la tarea.
- Se esfuerzan para salvar
obstáculos y dificultades.
- Disfrutan los resultados
personales en la realización de las tareas.
Dimensión 2. Autonomía.
- Resuelven las tareas de
forma creadora, sin limitarse a los procedimientos dados por la maestra.
- Aplican los procedimientos
estudiados sin necesidad de ayuda
Dimensión 3. Iniciativa.
- Asumen protagonismo en las
tareas de aprendizaje a partir de su propia iniciativa. (pp. 9- 10).
Al comparar los indicadores
presentados por ambos investigadores, es evidente que coinciden en varios
aspectos y que guardan estrecha relación con la realidad educativa cubana.
Cada una de las asignaturas
del currículo de una carrera universitaria juega su rol en la formación de la
independencia cognoscitiva de los estudiantes, así puede verse en el caso de
la Matemática.
El proceso de
enseñanza-aprendizaje de la Matemática
Cuba le ha otorgado gran
prioridad a la educación y dentro de ella reconoce la necesidad de elevar el
conocimiento de las ciencias, con énfasis en la Matemática.
Esta siempre ha sido una ciencia
útil para todos, pero de interés solo para una parte de los estudiantes;
mientras pocos la consideran fácil y atractiva, muchos la valoran de difícil y
compleja, su utilidad no es discutida por nadie, de ahí su prioridad en los
programas escolares de todos los niveles de educación.
Para comprender el
significado de la Matemática y su enseñanza, es necesario conocer su devenir
histórico, el cual muestra que los conocimientos matemáticos, surgidos de las
necesidades prácticas del hombre mediante un largo proceso de abstracción,
tienen un gran valor para la vida.
El estudio de las múltiples
aplicaciones de la Matemática en diferentes esferas de la vida económica,
cultural, militar y social, puede servir para comprender la necesidad de su
empleo en bien de la sociedad.
La aplicación de la
Matemática juega un importante papel en la planificación de la economía, la
dirección de la producción, el diagnóstico y tratamiento de enfermedades,
invadiendo así todos los campos del saber de la humanidad. A decir de Albarrán
y Suárez (2007):
En el perfeccionamiento continuo del Sistema Nacional de
Educación hay que tener en cuenta que (…) el programa de Matemática favorezca
la necesaria adaptación del contenido a nuestras realidades y condiciones
actuales (…). La meta es enseñarle al estudiante que no está en la escuela para
recibir órdenes, sino para descubrir cómo puede realizar tareas cada vez más
complejas usando sus propios recursos y pensamientos. (p. 43).
Tal concepción científica y
desarrolladora sobre el proceso de enseñanza-aprendizaje de la Matemática,
implica promover un aprendizaje reflexivo, interactivo, cooperativo en todos
los estudiantes, sin el cual se pierde el objetivo principal de la enseñanza de
esta asignatura. Hacer que los estudiantes aprendan a resolver problemas dados
en contextos diferentes, de modo que los conocimientos, habilidades, modos de
actividad mental y actitudes que se desea formar en ellos se adquieran mediante
el trabajo con problemas y en función de resolver estos.
Según Ballester (1995) “Las
formas de trabajo y de pensamiento matemático, requieren de los estudiantes una
constante actividad intelectual que exige analizar, comparar, fundamentar,
demostrar y generalizar, entre otras operaciones mentales” (p. 21).
En los últimos años, se han
incrementado los trabajos sobre la influencia del dominio afectivo en el
aprendizaje de la Matemática, al respecto Blanco, Cárdenas y Caballero (2015)
expresaron que:
Uno de los aspectos que actualmente se enfatiza y asume
en relación a la educación matemática en los currículos es la influencia de la
afectividad en los procesos de enseñanza y aprendizaje de las matemáticas. Y,
en particular, en la resolución de problemas (…) los factores cognitivos de
experiencia y los afectivos influencian el proceso de resolución de problemas
de matemáticas. Entre los afectivos se señalan explícitamente el interés, la
motivación, la presión, la ansiedad, el stress y la perseverancia. (p. 12).
Tal afirmación que comparten
los autores de la investigación refiere, entonces, que la responsabilidad fundamental
del maestro de Matemática es una labor educativa abarcadora: enseñar a los estudiantes
a pensar, motivarlos por la actividad que realizan, evaluar todo el proceso y
no solo el resultado de su actividad, por lo que entre los objetivos de su enseñanza
se destaca el aporte que debe ofrecer esta disciplina al desarrollo del pensamiento.
La Matemática en la
modalidad semipresencial del Curso por Encuentros, en las universidades, asume
la experiencia positiva del programa para exámenes de ingreso a la Educación Superior
en Cuba (a esta asignatura también se le conoce por Matemática Básica), con la
intención de contribuir al desarrollo de métodos para aprender a aprender. El
enfoque metodológico general de la asignatura lo constituye la resolución de
problemas, a partir de los cuales se fundamentan y consolidan los conceptos,
proposiciones y procedimientos. Igualmente posee amplias
potencialidades para el trabajo con las Tecnologías de la Informática y las
Comunicaciones.
En el programa de Matemática
elaborado para el Curso por Encuentros en la Universidad de Sancti Spíritus
“José Martí”, sus autoras: Garriga y Rodríguez (2016), del Departamento de
Matemática, hacen énfasis en que la asignatura resulta de gran importancia ya
que:
Permite
que los estudiantes sistematicen, profundicen y amplíen su saber acerca de los
contenidos de la enseñanza media básica y media superior, en tanto se
fundamentan desde el punto de vista de los dominios numéricos, trabajo
algebraico, ecuaciones, inecuaciones y sistemas de ecuaciones, las funciones,
la geometría y la trigonometría. Además, contribuye a que los estudiantes
desarrollen aún más sus habilidades y capacidades en la resolución y formulación
de problemas con un nivel de dificultad igual o superior a los que se
enfrentaron en los niveles de enseñanza precedentes. (p. 2).
Los investigadores de la Universidad de
Barcelona, Bados y García (2014), profesores de la Facultad de Psicología,
plantean que la solución de problemas es: “Un proceso
cognitivo-afectivo-conductual mediante el cual una persona intenta identificar
o descubrir una solución o respuesta de afrontamiento eficaz para un problema
particular” (p. METODOLOGÍA EMPLEADA
Como método general de la
investigación se utilizó el dialéctico materialista, a partir de su aplicación
en la transformación de la realidad objetiva de un grupo de estudiantes. Fueron
utilizados los métodos: histórico-lógico, para conocer la evolución y desarrollo
de la independencia cognoscitiva a través de la resolución de problemas; analítico–sintético
empleado en la fundamentación teórica de la independencia cognoscitiva de los
estudiantes y en la caracterización de los sustentos teóricos sobre los cuales
se basan las tareas de aprendizaje propuestas; del nivel empírico: observación
pedagógica y prueba pedagógica que permitieron aplicar técnicas afines: una
guía de observación y cuestionarios de preguntas, uno al inicio y otro después
de aplicada la propuesta para obtener información sobre la fase inicial del
diagnóstico y la evolución de la independencia cognoscitiva de los estudiantes
hacia el nivel deseado. El análisis documental se utilizó para el estudio de bibliografías
que fundamentan la independencia cognoscitiva en los estudiantes y su relación
con la resolución de problemas.
Constatación inicial sobre
el desarrollo de la independencia cognoscitiva a través de la resolución de problemas
En
el Centro Universitario Municipal de Fomento, durante el primer semestre del curso
2018-2019, se impartió la Matemática, basada en el programa para exámenes de
ingreso a la Educación Superior en Cuba, en el 1er año de tres carreras, con un
total de 30 estudiantes de matrícula.
En
estas carreras se profundizó en: cómo
mejorar la independencia cognoscitiva a través de la resolución de problemas,
para ello se analizaron sustentos teóricos básicos acerca de la dirección
del aprendizaje en la asignatura Matemática y las potencialidades y debilidades
de este grupo de estudiantes para resolver problemas de
la práctica escolar.
En esta medición se declaran indicadores a
partir de los conceptos de independencia cognoscitiva, la resolución de
problemas, la problemática que presentan los 30 estudiantes del Curso por Encuentros
en el 1er año de su carrera, tomados como muestra, y el enfoque metodológico
principal en la enseñanza de la Matemática. Los
indicadores presentados por Hernández et al. (2016) y Díaz (2011) se tuvieron
en cuenta al medir la calidad de la independencia cognoscitiva de los
estudiantes de la muestra, al elaborar la propuesta y al controlar el trabajo
independiente realizado a partir de cada tarea de aprendizaje.
En
la constatación inicial del diagnóstico, se aplicó una prueba pedagógica y una
guía de observación pedagógica.
Constatación
inicial del diagnóstico aplicado a los 30 estudiantes de la muestra
·
Nivel
de utilización de estrategias cognitivas para
resolver problemas. B—4; R—3; M—23.
· Nivel
de formulación de hipótesis relacionadas con el plan
de solución. B—4; R—3; M—23.
· Nivel de utilización de los conocimientos precedentes en la
ejecución del plan de solución. B—7; R—5; M—18.
· Nivel de análisis de gráficos, esquemas, modelos y figuras
tridimensionales. B—3; R—4; M—23.
· Nivel
de análisis de los resultados y la formulación de
conclusiones. B—8; R—5; M—17.
· Nivel
de participación en el debate sobre el mensaje educativo del problema mediante
una comunicación interactiva con los demás
estudiantes. B—3; R—5; M—22.
· Nivel
de motivación e interés cognitivo por resolver problemas. B—4; R—6; M—20.
· Nivel
de disposición para solucionar los problemas de manera independiente. B—3; R—5;
M—22.
De
los 30 estudiantes de la muestra hay cuatro que manifiestan con una adecuada
independencia cognoscitiva, cinco manifiestan necesidad de algún tipo de ayuda,
son inconstantes en su desempeño y no expresan con suficiente calidad sus
ideas. Los 21 restantes no tienen independencia cognoscitiva lo que se refleja
en que no están suficientemente motivados para resolver por sí solos los
problemas que se les presentan, necesitan mucha ayuda y no expresan con calidad
sus ideas en el debate sobre el mensaje educativo del problema a resolver.
Resumen
de las principales dificultades de los estudiantes, detectadas en la
fase inicial del diagnóstico:
·
Aplican
de manera incorrecta o no aplican las estrategias cognitivas para resolver
problemas.
·
Formulan
de manera incorrecta la hipótesis relacionada con el plan de solución.
·
Los
problemas relacionados con gráficos, esquemas, modelos y figuras
tridimensionales son enfrentados con carencias en los procedimientos de
solución.
·
En
el debate sobre el mensaje educativo de los problemas, carecen de los
conocimientos necesarios para mantener una participación activa.
·
La
disposición para resolver problemas de manera independiente, o sea sin niveles
de ayuda, carece de autonomía.
Para mejorar la
independencia cognoscitiva de los estudiantes de primer año del Curso por
Encuentros en el Centro Universitario de Fomento, desde la Matemática, fue
necesario llevarles una propuesta que permitiera aumentar su nivel de capacidad
y disposición para resolver problemas.
En el desarrollo de este artículo se
reelaboraron problemas matemáticos con la intención de utilizarlos
pedagógicamente para elevar el nivel de la independencia cognoscitiva en los
estudiantes de la muestra seleccionada. También, tiene su génesis en una línea
de trabajo metodológico desarrollada dentro de la universidad:
“La dirección del aprendizaje para el desarrollo de la independencia cognoscitiva
de los estudiantes desde la clase encuentro”.
RESULTADOS
Propuesta elaborada
para mejorar la independencia cognoscitiva de los estudiantes
La propuesta es tutelada por el profesor de
Matemática y en ella los estudiantes son puestos ante el reto de resolver
problemas matemáticos con varios incisos, en algunos de ellos, el
cuestionamiento está relacionado con la información general que se brinda en
el texto. Las tareas de aprendizaje, por sí solas no contribuyen a elevar el
nivel de independencia cognoscitiva sino que esta se mejora durante todo el
proceso de aprendizaje, a partir de la labor educativa. El accionar del
profesor en la orientación y control y el del estudiante en su trabajo
independiente y su autocontrol, juegan el rol más importante. En cada tarea de
aprendizaje, se propone un objetivo a cumplir y una metodología orientada por
el profesor para desarrollar el trabajo independiente; así como variadas formas
de control del resultado del trabajo realizado, de las habilidades en la independencia
cognoscitiva de los estudiantes y de la labor educativa inducida desde la
información general que brinda el problema. Para resolver las situaciones
problemáticas, se necesitan conocimientos básicos de Matemática, habilidades
para la búsqueda de información en textos impresos o en soporte electrónico y
conocimientos elementales de Lengua Materna para elaborar la respuesta a cada
interrogante. Las tareas de aprendizaje se deben resolver en el estudio
independiente y a través del desarrollo de todo el contenido de las tres primeras
unidades del programa de Matemática. Se aprovechan situaciones conocidas por
los estudiantes convirtiendo así a los problemas, que tienen que resolver, en
un reflejo de la realidad, de las relaciones entre objetos, procesos y
fenómenos afines a la economía, la política y la sociedad, propiciando también
la recopilación de información y datos; así como la labor educativa.
Piñeiro,
Pinto y Díaz (2015), hacen referencia a un modelo que se tuvo en cuenta en
el tratamiento de los problemas para que el estudiante remodele y examine sus
propias formas de pensar:
1. Familiarización con el problema:
· Trata
de entender a fondo la situación.
· Con
paz, con tranquilidad, a tu ritmo.
· Juega
con la situación, piérdele el miedo.
2. Búsqueda de una (s) estrategia (s):
· Empieza
por lo fácil.
· Experimenta.
· Haz
un esquema, una figura un diagrama.
· Escoge
un lenguaje adecuado, una notación apropiada.
· Busca
un problema semejante.
· Induce.
· Supongamos
el problema resuelto.
· Supongamos
que no está resuelto.
3. Lleva adelante tu estrategia
· Selecciona
las mejores ideas que se te han ocurrido en la fase anterior.
· Actúa
con flexibilidad. No te cierres en una idea, si las cosas se
complican busca otra vía.
· ¿Salió?
¿Seguro? Mira a fondo tu solución.
4. Revisa el proceso y saca consecuencia de él.
· Examina
a fondo el camino que has seguido. ¿Cómo has llegado a la
solución? ¿Por qué no has llegado?
· Trata
de entender no solo que la estrategia funciona sino por qué funciona.
· Examina
si encuentras un camino más simple.
· Mira
hasta dónde has usado un método.
· Reflexiona
sobre tu propio proceso de pensamiento y saca algunas conclusiones
y experiencias
para el futuro. (p. 6).
Se realizó un análisis del siguiente ejemplo:(Tomado
del texto de Matemática 9no grado, vigente en la educación cubana, cuyos
autores son Acosta, Quintana, Gort, Báez, Cantero, Cantón y Domínguez (2015).
Como
parte de la campaña de higienización de la ciudad, en un consejo popular se
formaron dos brigadas de fumigación contra el mosquito Aedes Aegypti. Un fin de
semana las dos brigadas fumigaron un total de 451 viviendas. Si la Brigada 1
hubiese fumigado 20 casas más ese fin de semana, entonces hubiese fumigado el
duplo de la cantidad de casas fumigadas por la Brigada 2. ¿Cuál de las dos
brigadas fumigó más cantidad de casas ese fin de semana?
Solución
Este problema es sobre la cantidad de casas
de un consejo popular que fumigan dos brigadas. En el texto se informa la
cantidad de casas que fumigaron en total estas dos brigadas y una relación entre
la cantidad de casas que fumigó cada una de estas, en la que aparecen las
palabras clave: más y duplo. Observa que para poder dar respuesta a la
interrogante del problema debes conocer la cantidad de casas que fumigó cada
brigada y las dos informaciones que aparecen en el texto te permiten establecer
dos relaciones de igualdad entre la cantidad de casas que fumigaron cada una de
las brigadas. Si asignas a la variable x la cantidad de casas fumigadas
por la Brigada 1 y a la variable y, la cantidad de casas fumigadas por
la Brigada 2 y realizas la transferencia del lenguaje común al algebraico las
dos relaciones que aparecen en el texto del problema, obtienes las ecuaciones:
x + y = 451, x + 20 =2y que conforman el sistema de dos ecuaciones lineales:
x: cantidad de casas
fumigadas por la Brigada 1
y:
cantidad de casas fumigadas por la Brigada 2
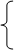 x
+ y = 451
x
+ y = 451
x + 20 =2y
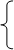
 x
+ y = 451
x
+ y = 451
x – 2y =-20 • (-1)
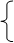 x
+ y = 451
x
+ y = 451
-x + 2y =20
3y = 471
y = 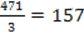
Sustituyendo
y= 157 en x + y = 451 se obtiene
x+ 157 = 451
x = 451 – 157
x = 294
Compruebas
en el texto del problema la solución encontrada. La Brigada 1 fumigó 294 casas
y la Brigada 2, 157. Pero, 294 + 157 =451 luego, las dos brigadas fumigaron 451
casas. Además, 294 + 20 = 314 y 2 • 157 = 314, por tanto, si la Brigada 1
hubiese fumigado 20 casas más, entonces hubiese fumigado el duplo de la
cantidad de casas fumigadas por la Brigada 2.
Respuesta:
La Brigada 1 fumigó más casas ese fin de semana. (p. 227).
Una acción realizada en el tratamiento de
este problema para contribuir más al logro de la independencia cognoscitiva y
como parte de la labor educativa es: agregar una pregunta que responde a la
búsqueda de un conocimiento adicional, muy importante en la formación integral
del estudiante. La pregunta puede ser: ¿por qué es necesario tener un control
higiénico en las casas y solares de cada consejo popular y además, fumigar si
encontramos un foco del mosquito Aedes Aegypti ? Elabora un párrafo con la
respuesta a esta pregunta, puedes auxiliarte para ello de la enciclopedia
cubana EcuRed.
La propuesta está conformada por varias
tareas de aprendizaje que contienen un problema cada una, pero con varios
incisos y uno de ellos está relacionado con una temática mencionada en el
problema, para ampliar conocimientos, indagar, buscar información en
enciclopedias u otras fuentes del conocimiento.
Tarea de Aprendizaje # 1
Título: El cultivo del café en
Cuba.
Objetivo: Interpretar el
problema matemático enunciado, de manera que puedas establecer las relaciones
necesarias para responder las preguntas y utilizando las Tecnologías de la
Informática y las comunicaciones (TIC), realiza una investigación sobre la
introducción del cultivo del café en Cuba.
Metodología: El profesor orienta
la actividad a partir de conformar tres equipos de trabajo por cada carrera.
Los estudiantes deben analizar el problema de manera individual, según los
pasos a seguir dispuestos por Piñero (2015): familiarizarse con el problema,
buscar una estrategia de solución, implementar la estrategia, revisar el
proceso de solución, sacar consecuencias de él y confrontar los resultados
obtenidos con los demás miembros del equipo. Investigar sobre el cultivo del
café en Cuba y su relación con la comunidad donde vive, como parte de la labor
educativa en su formación integral. Presentar el resultado de la investigación
en un evento científico en el grupo que será desarrollado a partir los
resultados obtenidos por cada equipo y en forma de panel.
Problema
1- En
tres días de labor, en la recogida de café, en fincas pertenecientes a
propietarios particulares en El Pedrero, provincia de Sancti Spíritus, un hombre
recolectó el lunes el 25 % de la meta que se propuso, el martes un  de
la misma y el miércoles cumplió, al recoger 70 kg.
de
la misma y el miércoles cumplió, al recoger 70 kg.
a-) Busca en internet el modelo a
seguir para resolver problemas, que aparece en el artículo titulado ¿Qué es la
resolución de problemas? De los autores Juan Luis Piñeiro, Eder Pinto y Danilo
Díaz–Levicoy, para guiarte al resolver el problema planteado. Está disponible
en: http://funes.uniandes.edu.co/6495/1/Pi%C3%B1eiro%2C_Pinto_y_D%C3%ADaz-Levicoy.pdf
b-) ¿Cuántos kilogramos debió recolectar en
los tres días?
c-) ¿Qué por ciento del total representa lo que
recolectó el miércoles?
d-) ¿Cuánto recolectó el lunes?
e-) ¿Cuál es el promedio de kilogramos
recolectados por día?
f-) Investiga sobre la historia de la
introducción del cultivo del café en Cuba y escribe una cuartilla sobre ello.
Conclusiones
Se realiza una valoración
colectiva sobre el tratamiento que le dieron a las diferentes acciones de
aprendizaje en las que intervinieron. Se le otorga una evaluación por equipo y
una individual a partir del nivel de participación en la tarea de aprendizaje.
Se orienta el trabajo independiente en función del contenido a tratar en la
próxima tarea de aprendizaje.
Tarea de Aprendizaje # 2
Título: El Pacto del Pedrero.
Objetivo: Resolver el
problema matemático enunciado, de manera que pueda establecer las relaciones
necesarias para responder las preguntas y realizar una investigación sobre la
significación histórica que tiene el Pacto del Pedrero para los cubanos.
Metodología: El profesor orienta
la actividad a partir de que los estudiantes deben resolver el problema buscando
una estrategia de solución correcta, implementar la estrategia, revisar el
proceso de solución, sacar consecuencias de él y además, como parte de la labor
educativa en su formación integral, investigar sobre el hecho histórico del
Pacto del Pedrero ocurrido en el municipio de Fomento en el año 1958, donde el
Che fue el protagonista principal. La solución del problema debe ser presentada
por cada equipo con el uso de una presentación electrónica donde un alumno
expondrá las respuestas a los tres primeros incisos y otro expondrá el
resultado de la investigación propuesta en el último inciso.
Problema
Como homenaje al comandante Ernesto Guevara
(Che), en la graduación de los estudiantes del duodécimo grado del Instituto
Preuniversitario Urbano “Olga Alonso” de Fomento, en el curso 2015-2016,
decidieron realizar un ascenso al histórico sitio de Caballete de Casa. En ese
lugar el Che tuvo su comandancia, al comenzar a organizar la lucha en la zona
central de Cuba, en el año 1958. Los graduados, para la subida, partieron de la
Tarja del Pacto del Pedrero, en la primera hora y media caminaron el 30% del
total del trayecto, en los 120 minutos siguientes recorrieron el 50% del
trayecto y en las 1,8h restantes, avanzaron los 3400 m que le faltaban para
llegar a la meta.
a)- ¿Cuántas horas demoró el ascenso,
incluyendo media hora de descanso, después de la primera etapa y una hora para
almorzar después de la segunda etapa?
b) -¿Qué distancia total recorrieron?
c) -¿Qué distancia recorrieron en la primera
etapa?
d)-Investiga sobre la significación histórica
que tiene el Pacto del Pedrero para los cubanos, en especial para los
espirituanos y redacta un texto de no más de dos cuartillas sobre el tema, el
cual se estructure en introducción, desarrollo y conclusiones.
Conclusiones
Se realiza una evaluación por equipo sobre el
tratamiento que le dieron a las diferentes acciones de aprendizaje en las que
intervinieron. Se le otorga una evaluación individual a cada estudiante a
partir de su nivel de participación en la tarea de aprendizaje. Se orienta la
nueva actividad.
Tarea de Aprendizaje # 3
Título: El cambio climático.
Objetivo: Analizar la situación
problemática planteada, de manera que pueda establecer las relaciones
necesarias para responder la pregunta propuesta, establer cuáles de las
regiones mencionadas son continentes e indagar sobre qué provoca la
ocurrencia del cambio climático y sus efectos negativos para nuestro planeta.
Metodología: El profesor orienta
la actividad a partir de que los estudiantes deben analizar el problema, familiarizarse
con la situación planteada, buscar una estrategia de solución e implementarla,
revisar el proceso de solución, sacar consecuencias de él y como parte dela
labor educativa en su formación integral, investigar sobre las regiones del
planeta Tierra reconocidas como continentes y sobre el cambio climático. La
revisión colectiva de la tarea que se realizará por equipos y en forma de Mesa
Redonda.
Problema
En una conferencia internacional sobre el
cambio climático, se reunieron 15 delegados de África, América, Asia y Europa.
Cada región envió una cantidad diferente de delegados y cada una estuvo representada
por lo menos por un delegado. América y Asia enviaron seis delegados, Asia y
Europa enviaron siete delegados.
a) ¿Qué región envió cuatro delegados?
b) Investiga sobre cuáles de estas regiones
son consideradas continentes.
c) Elabora una ponencia, en no más de cinco
cuartillas, con una hoja de presentación donde aparezca el tema: “El cambio
climático” y el autor. En las otras hojas debe aparecer: introducción,
desarrollo, conclusiones y bibliografía donde argumentes sobre qué provoca que
esto ocurra y sus efectos negativos en nuestro planeta.
Conclusiones
Se realiza una valoración colectiva sobre el
tratamiento que le dieron a las diferentes acciones de aprendizaje en las que
intervinieron. Se le otorga una evaluación por equipo y una individual a
partir del nivel de participación en la tarea de aprendizaje. Se orienta el
trabajo independiente en función del contenido a tratar en la próxima tarea de
aprendizaje.
Figura: Esquema
sobre la idea general de la propuesta.
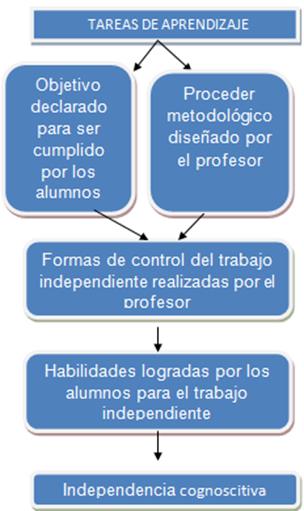
Fuente: elaboración propia
(2020)
DISCUSIÓN
Después de aplicada la propuesta
concebida, se tomó nuevamente la muestra de los 30 estudiantes y se les aplicó
una prueba pedagógica de salida y la guía de observación concebida.
Constatación final del diagnóstico aplicado a
los 30 estudiantes de la muestra
·
Nivel
de utilización de estrategias cognitivas para
resolver problemas. B--13; R-- 10; M—7.
· Nivel
de formulación de hipótesis relacionadas con el plan
de solución. B--12; R--9; M--9.
· Nivel
de utilización de los conocimientos precedentes en
la ejecución del plan de solución. B--15; R--7; M--8.
· Nivel de análisis de gráficos, esquemas, modelos y figuras
tridimensionales. B--13; R--12; M--5.
·
Nivel
de análisis de los resultados y la formulación de
conclusiones. B--12; R--8; M--10.
· Nivel
de participación en el debate sobre el mensaje educativo del problema mediante
una comunicación interactiva con los demás estudiantes.
B--18; R--9; M--3.
· Nivel
de motivación e interés cognitivo por resolver problemas. B--12; R--7; M--11.
· Nivel
de disposición para solucionar los problemas de manera independiente. B--15; R—10;
M--5.
De los 30 estudiantes de la muestra hay 12
que se manifiestan con una adecuada independencia cognoscitiva, ocho
manifiestan necesidad de algún tipo de ayuda, son inconstantes en su desempeño
y no expresan con suficiente calidad sus ideas. Los 10 restantes no tienen
independencia cognoscitiva lo que se refleja en que no están suficientemente
motivados para resolver por sí solos los problemas que se les presentan,
necesitan mucha ayuda y no expresan con calidad sus ideas en el debate sobre el
mensaje educativo del problema a resolver.
En el estudio realizado, sobre el tratamiento
del desarrollo de la independencia cognoscitiva desde una asignatura del
currículo de cada carrera, se pudo constatar que el sistema de influencias
desde la resolución de problemas fue efectivo, es evidente que hubo una mejora
con relación al estado inicial de la muestra. Las principales deficiencias
continúan en el nivel de independencia para la formulación de hipótesis relacionadas con el plan de solución, nivel
de independencia para el análisis de los resultados, la
formulación de conclusiones y el nivel de motivación e interés cognitivo
por resolver problemas.
CONCLUSIONES
La valoración de los fundamentos
teórico-metodológicos referentes al problema objeto de estudio, permite
reconocer que la resolución de problemas como capacidad matemática, contribuye
a mejorar la independencia cognoscitiva, teniendo en cuenta que este accionar
no puede convertirse en la realización de ejercicios rutinarios, sino en un
proceso en que el estudiante haga suyo los modos de actuación, incremente la
motivación por aprender por sí mismo y se inicie en la sistematización
continua de conocimientos y habilidades, incluyendo los procedimientos
heurísticos.
Al
concebir y aplicar las tareas, se dirigió el aprendizaje de la independencia
cognoscitiva a través de la selección del objetivo a lograr, la metodología a
desarrollar por el profesor, las formas de control y la labor educativa como
parte de su formación integral. Hubo un cambio cualitativo y cuantitativo
positivo al comparar el estado inicial y final, ya que se mejoró la
independencia cognoscitiva en los estudiantes universitarios de 1er año del Curso
por Encuentros en el Centro Universitario de Fomento.
REFERENCIAS
BIBLIOGRÁFICAS
Acosta, S., Quintana, A., Gort, M.,
Báez, L., Cantero, R. M., Cantón, J., y Domínguez, O. (2015). Matemática 9no
grado. La Habana, Cuba: Editorial Pueblo y Educación.
Albarrán, J. y Suárez, C. (2007). Desarrollo
de capacidades matemáticas en la escuela primaria. En Maestría en
Ciencias de la Educación. Mención Educación Primaria. Módulo III. Primera parte
(p. 39 - 64). La Habana, Cuba: Pueblo y Educación.
Álvarez de Zayas, C. (1998). Pedagogía
como Ciencia. (Epistemología de la Educación). Versión en soporte
magnético.
Bados, A. y García, E. (2014). Resolución de
problemas. Universidad de Barcelona, España. Recuperado de
diposit.ub.edu › dspace › bitstream
Ballester, S. (1995). La sistematización
de los conocimientos matemáticos. La Habana, Cuba: Editorial Academia.
Blanco, L., Cárdenas, J. A. y Caballero, A. (2015). La
resolución de problemas de matemáticas en la formación inicial de profesores de
Primaria. Universidad de Extremadura, España. Recuperado de http://mascvuex.unex.es/ebooks/sites/mascvuex.../Matematicas_9788460697602.pdf
Díaz, M. (2017). Ejercicios y problemas integradores
de Matemática para la Enseñanza Media Superior. La Habana, Cuba: Editorial
Pueblo y Educación.
Díaz, Y. (2011). Tareas de
aprendizaje para contribuir a la independencia cognoscitiva de los escolares de
sexto grado en la Educación Primaria (Tesis de maestría) Universidad
de Ciencias Pedagógicas “Capitán Silverio Blanco”, Sancti Spíritus, Cuba.
Garriga, A. T. y Rodríguez. C. (2016). Programa de la
asignatura Matemática Básica. Universidad de Sancti Spíritus “José Martí”,
Cuba.
Hernández, H., Cáceres, S., Barba, C. y
Losada, J. O., (2016). La independencia cognoscitiva desde postulados
integradores en la Universidad Técnica de Ambato, Ecuador. Congreso
Universidad Técnica de Ambato. Ambato, 5(1).
Recuperado de http://revista.congresouniversidad.cu/index.php/rcu/article/view/951
Martínez, S., Valdés, M. B. y Pérez, A.
(2017). Procedimientos metodológicos para el estudio de las magnitudes longitud
y tiempo en la educación primaria. Pedagogía y Sociedad, 20 (48), 77-97.
Recuperado de http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/514
Quero, O. y Ruiz, A. (2016). Transferencias
entre representaciones verbales de las secciones cónicas en la formación del
profesor de Matemática. Pedagogía y Sociedad, 19(47).
Recuperado
de http://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/499/400
Piñeiro, J. L., Pinto, E. y Díaz, D.
(2015). ¿Qué es la resolución de problemas? Redipe, 2 (4). Recuperado
de http://funes.uniandes.edu.co/6495/1/Pi%C3%B1eiro%2C_Pinto_y_D%C3%ADaz-Levicoy.pdf
Rodríguez, N. (2017). Perfeccionamiento
del trabajo independiente en el proceso de enseñanza-aprendizaje en la
Educación Médica, sustentado en las TIC. Conferencia. Universidad de
Ciencias Médicas de Santiago de Cuba. Recuperado de http://www.uvs.sld.cu/sites/default/files/usuarios/grisel/ti_y_tic.pdf
Varela, M. (2009). Aprendizaje independiente y aprendizaje
colaborativo en educación médica. Hospital General de México, 4 (72).
Recuperado de
www.medigraphic.com ›
hg-2009
Zavala, M. A., González, I. y Castro, M. A. (2019). La
innovación docente para la transformación de la enseñanza en el nivel superior.
Pedagogía y Sociedad, 54 (15), 1-8. Recuperado de https://revistas.uniss.edu.cu/index.php/pedagogia-y-sociedad/article/view/788
Zilberstein, J. (2009). Aprendizaje Desarrollador: Estrategias
de Aprendizaje en una Nueva Universidad. Curso de posgrado La Habana,
Cuba: Editorial Universitaria. Recuperado de
https://eduniv.reduniv.edu.cu
› fetchphp